bzoj1063【Noi2008】道路设计

题意：http://www.lydsy.com/JudgeOnline/problem.php?id=1063

　　　用一种划分方式将树划为重链和轻链，使得所有点到根节点的路径经过的轻链最大值最小

sol：  先判定图是否联通，若不连通输出-1

　　　考虑树形dp，f[i][j]表示以i为根的字树中到i的最大不便利值为j的方案数

　　　然而这时空都是O(n^2)的QAQ，而且没法转移

　　　考虑运用树链剖分的思想可证明，j之多为O(log2(n))的

　　　事实上，j在图为完全二叉树时取最大值O(log3(n))

　　　对于转移，f[i][j][k]表示以i为根值为j，i向儿子连了k条边的方案数

　　　

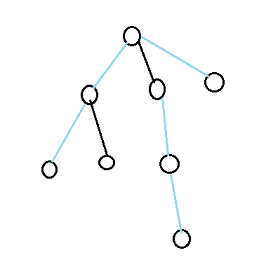
　　　则对于每个节点u，可以选择向(f1)或不向(f2)其某个儿子v连边

　　　则f1=f[v][j-1][0]+f[v][j-1][1]+f[v][j-1][2]　　（不向儿子连边）

　　　　f2=f[v][j][0]+f[v][j][1]　　（向儿子连边）

　　　对于某个点，在遍历到他的一个儿子时，之前儿子的影响已经被累加进答案f[u][j][]

　　　考虑新加进来的点的影响(为避免后效性应按2-1-0的顺序计算)：

　　　　f[u][j][2]=f[u][j][2]*f1+f[u][j][1]*f2

　　　　f[u][j][1]=f[u][j][1]*f1+f[u][j][0]*f2

　　　　f[u][j][0]=f[u][j][0]*f1

　　　最后从小到大扫一遍j，如果有，输出即可，注意%Q等于0的情况(设为Q)

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int Mx=;
int n,m,Q,tot,head[Mx],ver[Mx],next[Mx];
long long ans,f[Mx][][];
inline long long jud(long long tmp)//处理%Q=0的情况
{
    if(tmp!=&&tmp%Q==) return Q;
    else return tmp%Q;
}
inline void add(int x,int y)
{
    tot++;
    next[tot]=head[x];
    ver[tot]=y;
    head[x]=tot;
}
void dfs(int x,int fa)
{
    int cnt=;//cnt记录儿子个数
    for(int i=head[x];i;i=next[i])
        if(ver[i]!=fa)
            dfs(ver[i],x),cnt++;
    for(int j=;j<=;j++) f[x][j][]=;//f数组赋初值
    if(cnt==) return ;//叶子节点
    for(int i=head[x];i;i=next[i])//树形dp
        if(ver[i]!=fa)
        {
            int y=ver[i];
            for(int j=;j<=;j++)
            {
                long long f1,f2;
                f1=f[y][j-][]+f[y][j-][]+f[y][j-][];
                f2=f[y][j][]+f[y][j][];
                f[x][j][]=jud((long long) f[x][j][]*f1+(long long) f[x][j][]*f2);
                f[x][j][]=jud((long long) f[x][j][]*f1+(long long) f[x][j][]*f2);
                f[x][j][]=jud((long long) f[x][j][]*f1);
            }
        }

}
int main()
{
    scanf("%d%d%d",&n,&m,&Q);
    for(int i=;i<=m;i++)
    {
        int x,y;scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    if(m<n-) { puts("-1\n-1"); return ; }
    dfs(,);
    for(int j=;j<=;j++)
    {
        ans=f[][j][]+f[][j][]+f[][j][];
        if(ans!=)
        {
            cout<<j<<endl<<(ans%Q)<<endl;
            return ;
        }
    }
    return ;
}