汇编4OPCODE

opcode原理

前缀域

• 切换操作数大小前缀 : 066h

  • 可以将32位的操作数切换成16位的操作数

B8 00010000 | MOV EAX,0x100     
66:B8 0001  | MOV AX,0x100  
​
8918        | MOV DWORD PTR DS:[EAX],EBX  
66:8918     | MOV WORD PTR DS:[EAX],BX 

• 切换地址大小(切换寻址模式) : 067h

  • 用于将32位存储器的寻址方式切换成16位的寻址方式(16位的存储器寻址方式中,只能使用bx,si,di,bp寄存器作为内存地址) , 而32位汇编中,可以使用任意寄存器.

66:8918    | MOV WORD PTR DS:[EAX],BX   
67:8918    | MOV DWORD PTR DS:[BX+SI],EBX

• 重复操作前缀:0f2h,0f3h

F2:A4      | REPNE MOVSB     
F3:A4      | REP MOVSB     
F2:45      | INC EBP    ; 没有起作用  

• 修改默认段:

3E:8945 00| MOV DWORD PTR DS:[EBP],EAX;3E->ds
26:8918   | MOV DWORD PTR ES:[EAX],EBX;26->es
36:8918   | MOV DWORD PTR SS:[EAX],EBX;36->ss
2E:8918   | MOV DWORD PTR CS:[EAX],EBX;2E->cs
64:8918   | MOV DWORD PTR FS:[EAX],EBX;64->fs
65:8918   | MOV DWORD PTR GS:[EAX],EBX;65->gs

机器码翻译成反汇编的方法

83C404A178812801A35481280168548128018B0D7481280151684881280168448128016840812801FF15A4922801

1. 查表(intel提供的1字节指令映射表)

   1. 将第一个字节取出, 取查表(例如 83h)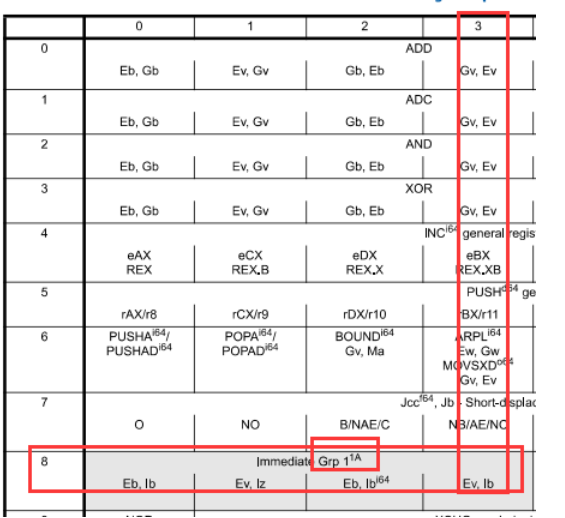
      

      

   2. 以高4位作为y轴,以低4位作为x轴, 坐标相交之处,就是这个code域对应的指令了, 如果查找的是group,那么还需要进一步去查group表,(依然使用机器码去查)
      

      

      1. 接着需要用83h的下一个字节(C4)作为modR/M域再进一步确认使用group中的哪一个. 将c4展开为二进制11000100

   3. 无论是直接在1字节对照表中,还是在group表中, 得到的都是指令格式: ADD Ev,Ib

      格式解析:

      1. ADD - 指令的助记符

      2. Ev,Ib 说明指令有两个操作数

      3. E - 第一个操作数是寄存器或内存操作数

      4. v - 第一个操作数的大小和当前处理器模式一样(32位时,操作数大小就是32位的)

      5. I - 第二个操作数是一个立即数, 说明在指令的modR/M域后面还有一个Imm域, 保存着指令的立即数操作数(立即数域:04)

      6. b-立即数的大小是一个字节. 说明立即数域的长度是1字节

   4. 目前可以确认指令是: Add Ev,04

   5. Ev中使用的寄存器的名字, 由modR/M域来提供. 需要去查询modR/M表

      1. modR/M表的组成:

         1. 表的左列, 是寄存器或内存操作, 在表的顶列,是纯寄存器操作数.

         2. 当操作数的类型是G的时候, 表示操作是纯寄存器. 应当到表的顶列去取出寄存器的名字.

         3. 当操作数的类型是E的时候, 表示操作数可能是寄存器,可能是存储器, 应当在表的左列取出操作数.

         4. 无论在那列, 都有很多寄存器, 此时需要使用操作数的大小来选择一款寄存器.
            

      

   6. 当前求出的指令就是: Add esp , 04;

2. ModR/M域保存着指令的比较复杂的寻址方式。它携带着一下信息

   1. 操作数名称（寄存器、内存地址）

   2. 是否存在SIB域

   3. 是否存在相对偏移

      ModR/M域占一个字节，可以将这一个字节拆分成一下格式。

      89 D8 move eax，eb

      D8=11011000

      Mod Reg R/M

      11 011 000

3. SIB域主要保存那些寄存器寻址的操作数中，带有乘法运算的部分。

   例如：mov eax，[ebx*4]

13字节汇编指令的赏析

LOCK MOV DWORD PTR ES:[EDX*4+ECX+0AA],11

F0:26:C7 87 91 AA000000 11000000

前缀 OPCODE MODR/M SIB DISPLACEMENT IMMEDIATE

F0:26 C7 84 91 AA000000 11000000

解析例子

​
;例子1
​
83C404 
A178812801 
A354812801
6854812801
8B0D74812801
51684881280168448128016840812801FF15A4922801
​
code域: A1 
mov eax,Ov
O - 存储器直接寻址方式, 
    说明指令的下一个字节就是一个内存地址
v - 操作数的大小就是`dword ptr`
mov eax,dword ptr[0x01288178]
​
code域: A3
mov Ov,eax
mov dword ptr[0x1288154],eax
​
6854812801
code域: 68
push Iz
I - 立即数
z - 
push 1288154
​
​
​
8B0D74812801
code域: 8B
    Mov Gv,Ev
ModR/M域: 0D
Gv : 在表的顶部: ecx
Ev : 在表的左边: disp32 - 偏移域
偏移域 : 74812801=>0x01288174
mov ecx,[0x1288174]
​
​
; 例子2
​
C7048100100000
C784810010000000100000
898C8100100000
​
code: C7 => mov Ev,Iz
modR/M: 04  
            Ev => [--][--]
SIB : 81    左边找到的寄存器 + 顶上找到的寄存器
            然后将找到寄存器作为存储器寻址方式写上
            eax*4+ecx
mov [eax*4+ecx] ,01000h
​
code: C7 => mov Ev,Iz
modR/M: 84  
            Ev => [--][--]+disp32
SIB : 81 =>  eax*4+ecx  
disp32 : 00100000 => 1000h
    [--][--]+disp32 => [ eax*4+ecx+01000h]
Iz : 00100000
最终的指令: mov [eax*4+ecx+01000h],01000h
​
 
code : 89 => Mov Ev,Gv
modR/M: 8C => 
            Ev => [--][--]+disp32
            Gv => ecx
SIB : 81  =>  eax*4+ecx 
disp32    => 00100000
最终的指令 :Mov [eax*4+ecx+01000h],ecx
​
​
; 例子3
​
E912563545
E865123314
FF2556781234
​
code:E9 => jmp Jz
    J => 操作是一个偏移值(立即数)
    z => 32位
最终的指令:
    jmp eip+45355612+5(指令自身长度)
​
code : E8 => call jz
最终的指令:
    call eip+14331265+5
​
code FF: 
modR/M 25 -> 00100101 => jmp Ev
    Ev => disp32
disp32 => 56781234 => 034127856h
最终的指令
        jmp [034127856h]