有向图强连通分量的Tarjan算法（转）

[有向图强连通分量]

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

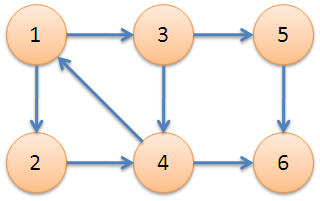
直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。

[Tarjan算法]

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号（这个好像有点问题，原文评论说改为：low(u)为u或u的子树通过最多一条反向边能够追溯到的最早的栈中节点的次序号。好像对？）。由定义可以得出，

Low(u)=Min
{
　　DFN(u),
　　DFN(v),//(u,v)为指向栈中节点的后向边(非横叉边)
　　Low(v)//(u,v)为树枝边，u为v的父节点
}

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

算法伪代码如下

tarjan(u)
{
    DFN[u]=Low[u]=++Index                      // 为节点u设定次序编号和Low初值
    Stack.push(u)                              // 将节点u压入栈中
    for each (u, v) in E                       // 枚举每一条边
        if (v is not visted)               // 如果节点v未被访问过
            tarjan(v)                  // 继续向下找
            Low[u] = min(Low[u], Low[v])
        else if (v in S)                   // 如果节点v还在栈内
            Low[u] = min(Low[u], DFN[v])
    if (DFN[u] == Low[u])                      // 如果节点u是强连通分量的根
        repeat
            v = S.pop                  // 将v退栈，为该强连通分量中一个顶点
            print v
        until (u== v)
}

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

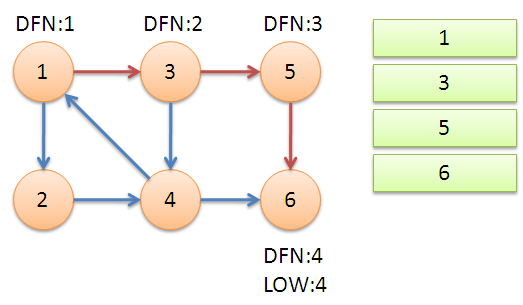
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

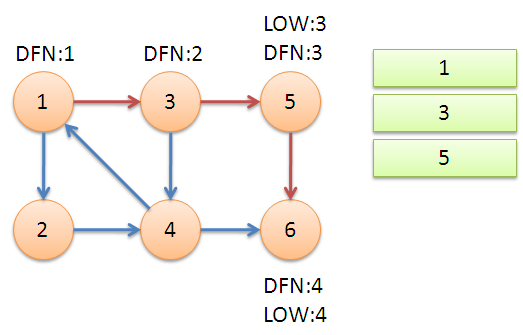
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

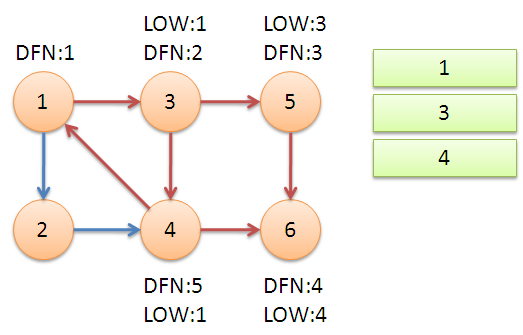
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

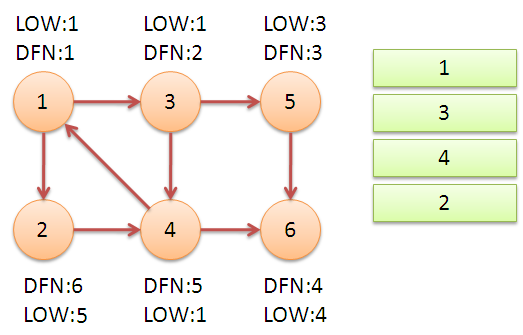
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

求有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。 在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。

附：tarjan算法的C++程序

void tarjan(int i)
{
    int j;
    DFN[i]=LOW[i]=++Dindex;
    instack[i]=true;
    Stap[++Stop]=i;
    for (edge *e=V[i];e;e=e->next)
    {
        j=e->t;
        if (!DFN[j])
        {
            tarjan(j);
            if (LOW[j]<LOW[i])
                LOW[i]=LOW[j];
        }
        else if (instack[j] && DFN[j]<LOW[i])
            LOW[i]=DFN[j];
    }
    if (DFN[i]==LOW[i])
    {
        Bcnt++;
        do
        {
            j=Stap[Stop--];
            instack[j]=false;
            Belong[j]=Bcnt;
        }
        while (j!=i);
    }
}
void solve()
{
    int i;
    Stop=Bcnt=Dindex=;
    memset(DFN,,sizeof(DFN));
    for (i=;i<=N;i++)
        if (!DFN[i])
            tarjan(i);
}

[参考资料]

• Wikipedia
• Amber的图论总结

 

转自：https://www.byvoid.com/en/blog/scc-tarjan