Space Ant（极角排序）

Space Ant

http://poj.org/problem?id=1696

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5371		Accepted: 3343

Description

The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations: 

1. It can not turn right due to its special body structure.
2. It leaves a red path while walking.
3. It hates to pass over a previously red colored path, and never does that.

The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y. 
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance. 
The problem is to find a path for an M11 to let it live longest. 
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.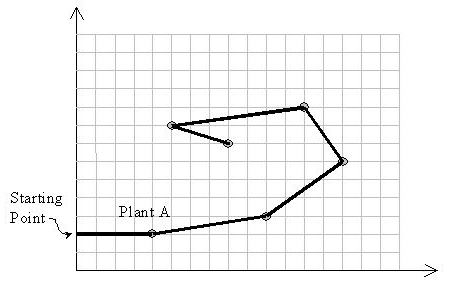 

Input

The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.

Output

Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.

Sample Input

2
10
1 4 5
2 9 8
3 5 9
4 1 7
5 3 2
6 6 3
7 10 10
8 8 1
9 2 4
10 7 6
14
1 6 11
2 11 9
3 8 7
4 12 8
5 9 20
6 3 2
7 1 6
8 2 13
9 15 1
10 14 17
11 13 19
12 5 18
13 7 3
14 10 16

Sample Output

10 8 7 3 4 9 5 6 2 1 10
14 9 10 11 5 12 8 7 6 13 4 14 1 3 2

找到最左下的点，然后对极角排序即可

 #include<cstdio>
 #include<iostream>
 #include<vector>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 const double eps=1e-;
 const double INF=1e20;
 const double PI=acos(-1.0);
 const int maxp=;
 int sgn(double x){
     if(fabs(x)<eps) return ;
     if(x<) return -;
     else return ;
 }
 inline double sqr(double x){return x*x;}
 struct Point{
     int pos;
     double x,y;
     Point(){}
     Point(double _x,double _y){
         x=_x;
         y=_y;
     }
     void input(){
         scanf("%lf %lf",&x,&y);
     }
     void output(){
         printf("%.2f %.2f\n",x,y);
     }
     bool operator == (const Point &b)const{
         return sgn(x-b.x) ==  && sgn(y-b.y)== ;
     }
     bool operator < (const Point &b)const{
         return sgn(x-b.x)==?sgn(y-b.y)<:x<b.x;
     }
     Point operator - (const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     //叉积
     double operator ^ (const Point &b)const{
         return x*b.y-y*b.x;
     }
     //点积
     double operator * (const Point &b)const{
         return x*b.x+y*b.y;
     }
     //返回长度
     double len(){
         return hypot(x,y);
     }
     //返回长度的平方
     double len2(){
         return x*x+y*y;
     }
     //返回两点的距离
     double distance(Point p){
         return hypot(x-p.x,y-p.y);
     }
     Point operator + (const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator * (const double &k)const{
         return Point(x*k,y*k);
     }
     Point operator / (const double &k)const{
         return Point(x/k,y/k);
     }

     //计算pa和pb的夹角
     //就是求这个点看a,b所成的夹角
     ///LightOJ1202
     double rad(Point a,Point b){
         Point p=*this;
         return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p)));
     }
     //化为长度为r的向量
     Point trunc(double r){
         double l=len();
         if(!sgn(l)) return *this;
         r/=l;
         return Point(x*r,y*r);
     }
     //逆时针转90度
     Point rotleft(){
         return Point(-y,x);
     }
     //顺时针转90度
     Point rotright(){
         return Point(y,-x);
     }
     //绕着p点逆时针旋转angle
     Point rotate(Point p,double angle){
         Point v=(*this) -p;
         double c=cos(angle),s=sin(angle);
         return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
     }
 };

 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e){
         s=_s;
         e=_e;
     }
     bool operator==(Line v){
         return (s==v.s)&&(e==v.e);
     }
     //根据一个点和倾斜角angle确定直线，0<=angle<pi
     Line(Point p,double angle){
         s=p;
         if(sgn(angle-PI/)==){
             e=(s+Point(,));
         }
         else{
             e=(s+Point(,tan(angle)));
         }
     }
     //ax+by+c=0;
     Line(double a,double b,double c){
         if(sgn(a)==){
             s=Point(,-c/b);
             e=Point(,-c/b);
         }
         else if(sgn(b)==){
             s=Point(-c/a,);
             e=Point(-c/a,);
         }
         else{
             s=Point(,-c/b);
             e=Point(,(-c-a)/b);
         }
     }
     void input(){
         s.input();
         e.input();
     }
     void adjust(){
         if(e<s) swap(s,e);
     }
     //求线段长度
     double length(){
         return s.distance(e);
     }
     //返回直线倾斜角 0<=angle<pi
     double angle(){
         double k=atan2(e.y-s.y,e.x-s.x);
         if(sgn(k)<) k+=PI;
         if(sgn(k-PI)==) k-=PI;
         return k;
     }
     //点和直线的关系
     //1 在左侧
     //2 在右侧
     //3 在直线上
     int relation(Point p){
         int c=sgn((p-s)^(e-s));
         if(c<) return ;
         else if(c>) return ;
         else return ;
     }
     //点在线段上的判断
     bool pointonseg(Point p){
         return sgn((p-s)^(e-s))==&&sgn((p-s)*(p-e))<=;
     }
     //两向量平行(对应直线平行或重合)
     bool parallel(Line v){
         return sgn((e-s)^(v.e-v.s))==;
     }
     //两线段相交判断
     //2 规范相交
     //1 非规范相交
     //0 不相交
     int segcrossseg(Line v){
         int d1=sgn((e-s)^(v.s-s));
         int d2=sgn((e-s)^(v.e-s));
         int d3=sgn((v.e-v.s)^(s-v.s));
         int d4=sgn((v.e-v.s)^(e-v.s));
         if((d1^d2)==-&&(d3^d4)==-) return ;
         return (d1==&&sgn((v.s-s)*(v.s-e))<=||
                 d2==&&sgn((v.e-s)*(v.e-e))<=||
                 d3==&&sgn((s-v.s)*(s-v.e))<=||
                 d4==&&sgn((e-v.s)*(e-v.e))<=);
     }
     //直线和线段相交判断
     //-*this line -v seg
     //2 规范相交
     //1 非规范相交
     //0 不相交
     int linecrossseg(Line v){
         int d1=sgn((e-s)^(v.s-s));
         int d2=sgn((e-s)^(v.e-s));
         if((d1^d2)==-) return ;
         return (d1==||d2==);
     }
     //两直线关系
     //0 平行
     //1 重合
     //2 相交
     int linecrossline(Line v){
         if((*this).parallel(v))
             return v.relation(s)==;
         return ;
     }
     //求两直线的交点
     //要保证两直线不平行或重合
     Point crosspoint(Line v){
         double a1=(v.e-v.s)^(s-v.s);
         double a2=(v.e-v.s)^(e-v.s);
         return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
     }
     //点到直线的距离
     double dispointtoline(Point p){
         return fabs((p-s)^(e-s))/length();
     }
     //点到线段的距离
     double dispointtoseg(Point p){
         if(sgn((p-s)*(e-s))<||sgn((p-e)*(s-e))<)
             return min(p.distance(s),p.distance(e));
         return dispointtoline(p);
     }
     //返回线段到线段的距离
     //前提是两线段不相交，相交距离就是0了
     double dissegtoseg(Line v){
         return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e)));
     }
     //返回点P在直线上的投影
     Point lineprog(Point p){
         return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2()));
     }
     //返回点P关于直线的对称点
     Point symmetrypoint(Point p){
         Point q=lineprog(p);
         return Point(*q.x-p.x,*q.y-p.y);
     }
 };

 Line L[];
 int book[];
 int n;

 bool Check(Line a,Line b){
     if(sgn((a.s-a.e)^(b.s-a.e))*sgn((a.s-a.e)^(b.e-a.e))>) return false;
     if(sgn((b.s-b.e)^(a.s-b.e))*sgn((b.s-b.e)^(a.e-b.e))>) return false;
     if(sgn(max(a.s.x,a.e.x)-min(b.s.x,b.e.x))>=&&sgn(max(b.s.x,b.e.x)-min(a.s.x,a.e.x))>=
      &&sgn(max(a.s.y,a.e.y)-min(b.s.y,b.e.y))>=&&sgn(max(b.s.y,b.e.y)-min(a.s.y,a.e.y))>=)
         return true;
     else return false;
 }

 Point p[];
 int pos;

 double dist(Point a,Point b){
     return (b-a)*(b-a);
 }

 bool cmp(Point a,Point b){
     double tmp=(a-p[pos])^(b-p[pos]);
     if(sgn(tmp)>){
         return true;
     }
     else if(sgn(tmp)<){
         return false;
     }
     else return dist(p[pos],a)<dist(p[pos],b);
 }

 int main(){
     int T;
     std::ios::sync_with_stdio(false);
     cin>>T;
     while(T--){
         int n;
         cin>>n;
         pos=;
         for(int i=;i<=n;i++){
             cin>>p[i].pos>>p[i].x>>p[i].y;
         }
         Point tmp=p[];
         int pp=;
         for(int i=;i<=n;i++){
             if((p[i].y<tmp.y)||(p[i].y==tmp.y&&p[i].x<tmp.x)){
                 tmp=p[i];
                 pp=i;
             }
         }
         swap(p[pp],p[]);
         vector<int>ve;
         ve.push_back(p[].pos);
         for(int i=;i<n;i++){
             sort(p+pos,p+n+,cmp);
             pos++;
             ve.push_back(p[pos].pos);
         }
         cout<<n;
         for(int i=;i<ve.size();i++){
             cout<<" "<<ve[i];
         }
         cout<<endl;
     }
     return ;
 }