计蒜客 31459 - Trace - [线段树][2018ICPC徐州网络预赛G题]

题目链接：https://nanti.jisuanke.com/t/31459

样例输入

3
1 4
4 1
3 3

样例输出

10

题意：

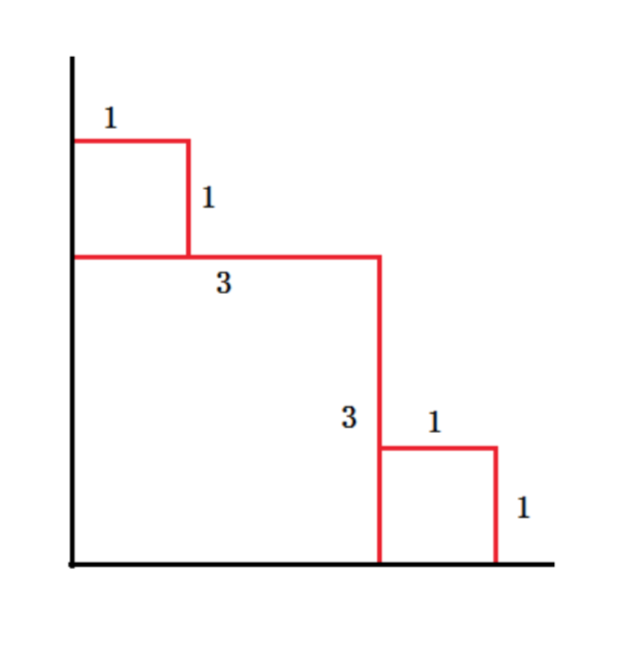
二维平面上给出 $n$ 个点，每个点坐标 $\left( {x,y} \right)$ 代表一个从原点到 $\left( {x,y} \right)$ 的长方形，

其中标记红线为线段 $\left( {x,0} \right)\left( {x,y} \right)$ 和 $\left( {0,y} \right)\left( {x,y} \right)$，

每次往二维平面上放置长方形会覆盖住之前放置的长方形，求 $n$ 个长方形全部放置完之后，整个图形上剩余的红线的总长度。

题解：

$x$ 方向和 $y$ 方向可以分开来看，分成 $n$ 个平行于 $x$ 轴的线段和 $n$ 个平行于 $y$ 轴的线段，

不妨看 $n$ 个平行于 $x$ 轴的线段（平行 $x$ 轴的和平行 $y$ 轴的计算方式是一样的），

对于第 $i$ 条线段，其后面的第 $i+1$ 到 第$n$ 条线段，若他们的 $y$ 坐标大于等于当前线段，那么就会覆盖掉一部分（乃至全部）的当前线段，

我们只要找出：第 $i+1$ 到 第$n$ 条线段中，满足 $y$ 坐标大于等于当前线段的，最长的那一条（$x$ 值最大的那一条），

这条线段的 $x$ 值，决定了当前第 $i$ 条线段被覆盖掉了多少，那么剩下的就是对答案的贡献，

所以我们从 $n$ 开始递减枚举，用线段树维护区间最大值（当然，坐标需要离散化，否则太大了），不断累加每条线段的贡献即可。

时间复杂度 $O\left( {n\log n} \right)$。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int maxn=5e4+;

int n;
struct Point{
    ll x,y;
}p[maxn];

vector<ll> x;
inline int getxid(int val){return lower_bound(x.begin(),x.end(),val)-x.begin();}

vector<ll> y;
inline int getyid(int val){return lower_bound(y.begin(),y.end(),val)-y.begin();}

/********************************* Segment Tree - st *********************************/
struct Node{
    int l,r;
    int val;
}node[*maxn];
void pushup(int root)
{
    node[root].val=max(node[root*].val,node[root*+].val);
}
void build(int root,int l,int r)
{
    if(l>r) return;
    node[root].l=l; node[root].r=r;
    node[root].val=;
    if(l==r) return;
    else
    {
        int mid=l+(r-l)/;
        build(root*,l,mid);
        build(root*+,mid+,r);
        pushup(root);
    }
}
void update(int root,int pos,int val)
{
    if(node[root].l==node[root].r)
    {
        node[root].val=max(node[root].val,val);
        return;
    }
    int mid=node[root].l+(node[root].r-node[root].l)/;
    if(pos<=mid) update(root*,pos,val);
    if(pos>mid) update(root*+,pos,val);
    pushup(root);
}
int askmax(int root,int st,int ed)
{
    if(st>node[root].r || ed<node[root].l) return -INF;
    if(st<=node[root].l && node[root].r<=ed) return node[root].val;
    else return max(askmax(root*,st,ed),askmax(root*+,st,ed));
}
/********************************* Segment Tree - ed *********************************/

int main()
{
    scanf("%d",&n);

    x.clear(); x.push_back();
    y.clear(); y.push_back();
    for(int i=;i<=n;i++)
    {
        scanf("%lld%lld",&p[i].x,&p[i].y);
        x.push_back(p[i].x);
        y.push_back(p[i].y);
    }
    sort(x.begin(),x.end());
    x.erase(unique(x.begin(),x.end()),x.end());
    sort(y.begin(),y.end());
    y.erase(unique(y.begin(),y.end()),y.end());

    build(,,y.size());
    ll X=;
    for(int i=n;i>=;i--)
    {
        int yid=getyid(p[i].y);
        int xid=getxid(p[i].x);
        int mx=askmax(,yid,y.size());
        if(xid>mx) X+=(ll)(p[i].x-x[mx]);
        update(,yid,xid);
    }

    build(,,x.size());
    ll Y=;
    for(int i=n;i>=;i--)
    {
        int yid=getyid(p[i].y);
        int xid=getxid(p[i].x);
        int my=askmax(,xid,x.size());
        if(yid>my) Y+=(ll)(p[i].y-y[my]);
        update(,xid,yid);
    }
    cout<<X+Y<<endl;
}