长短时记忆网络(LSTM)

长短时记忆网络

循环神经网络很难训练的原因导致它的实际应用中很处理长距离的依赖。本文将介绍改进后的循环神经网络：长短时记忆网络(Long Short Term Memory Network, LSTM)，

原始RNN的隐藏层只有一个状态，即h，它对于短期的输入非常敏感。那么如果我们再增加一个状态，即c，让它来保存长期的状态，这就是长短时记忆网络。

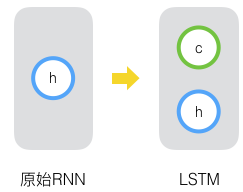
新增加的状态c，称为单元状态。我们把上图按照时间维度展开：

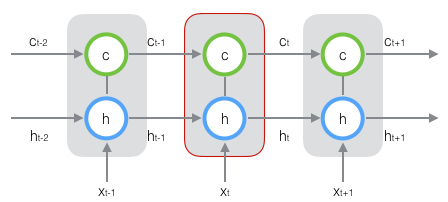
可以看到在t时刻，LSTM的输入有三个：当前时刻网络的输出值$x_t$、上一时刻LSTM的输出值$h_{t-1}$、以及上一时刻的单元状态$c_{t-1}$；LSTM的输出有两个：当前时刻LSTM输出值$h_t$、和当前时刻的单元状态$x_t$。注意$x、h、c$都是向量。

LSTM的关键，就是怎样控制长期状态c。在这里，LSTM的思路是使用三个控制开关。第一个开关，负责控制继续保存长期状态c；第二个开关，负责控制把即时状态输入到长期状态c；第三个开关，负责控制是否把长期状态c作为当前的LSTM的输出。三个开关的作用如下图所示：

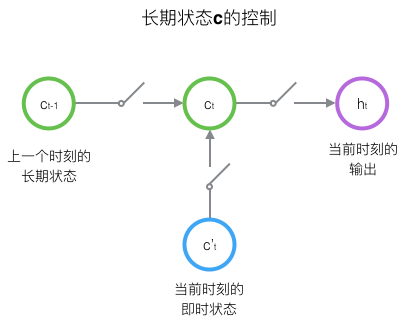
接下来我们要描述一下，输出h和单元状态c的具体计算方法。

长短时记忆网络的前向计算

我们引入“门(gate)”的概念。门实际上就是一层全连接层，它的输入是一个向量，输出是一个0到1之间的实数向量。假设W是门的权重向量，$b$是偏置项，那么门可以表示为：

$$g(x)=\sigma (Wx+b)$$

　　门的输出是0到1之间的实数向量，用门向量的输出向量按元素乘以我们需要控制的那个向量，当门输出为0时，任何向量与之相乘都会得到0向量，这就相当于啥都不能通过；输出为1时，任何向量与之相乘都不会有任何改变，这就相当于啥都可以通过。因为$\sigma$（也就是sigmoid函数）的值域是(0,1)，所以门的状态都是半开半闭的。

LSTM用两个门来控制单元状态c的内容，一个是遗忘门，它决定了上一时刻的单元状态$c_{t-1}$有多少保留到当前时刻$c_t$；另外一个是输出门，他决定了当前时刻网络的输入$x_t$有多少保存到单元状态$c_t$。LSTM用输出门来控制单元状态$c_t$有多少输出到LSTM的当前输出值$h_t$。LSTM用输出门来控制单元状态$c_t$有多少输出到LSTM的当前输出值$h_t$。

遗忘门的表达式是：

$$athbf{f}_t=\sigma(W_f\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_f)\qquad\quad(式1)$$

上式中，$W_f$是遗忘门的权重矩阵，$h_{t-1,x_t}$表示把两个向量连接成一个更长的向量，$b_f$是遗忘门的偏置项，$\sigma$是sigmoid函数。如果输入的维度是$d_x$，隐藏层的维度是$d_h$，单元状态的维度是$d_c$(d_c=d_h)，则遗忘门的权重矩阵$W_f$维度是$d_c x (d_h+d_x)$。事实上，权重矩阵$W_f$都是两个矩阵拼接而成的：一个是$W_{fh}$，它对应着输入项$h_{t-1}$，其维度为$d_cxd_h$；一个是$W_{fx}$，它对应着输入项$x_t$，其维度为$d_c x d_x$。$W_f$可以写为：

$$\begin{align}
\begin{bmatrix}W_f\end{bmatrix}\begin{bmatrix}\mathbf{h}_{t-1}\\
\mathbf{x}_t\end{bmatrix}&=
\begin{bmatrix}W_{fh}&W_{fx}\end{bmatrix}\begin{bmatrix}\mathbf{h}_{t-1}\\
\mathbf{x}_t\end{bmatrix}\\
&=W_{fh}\mathbf{h}_{t-1}+W_{fx}\mathbf{x}_t
\end{align}$$

下图显示了遗忘门的计算：

接下来看看输入门：

$$\mathbf{i}_t=\sigma(W_i\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_i)\qquad\quad(式2)$$

上式中，$W_i$是输入门的权重矩阵，$b_i$是输入门的偏置项。下图表示了输入门的计算：

接下来，我们计算用于描述当前输入的单元状态$\tilde{c}_t$，它是根据上一次的输出和本次输入来计算的：

$$\mathbf{\tilde{c}}_t=\tanh(W_c\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_c)\qquad\quad(式3)$$

下图是$\tilde{c}_t$的计算：

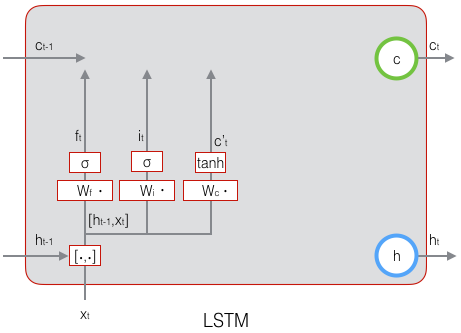
现在，我们计算当前时刻的单元状态$c_t$。它是由上一次的单元状态$c_{t-1}$按元素乘以遗忘门$f_t$，再用当前输入的单元状态$\tilde{c}_t$按元素乘以输入门$i_t$，再将两个积加和产生的：

$$\mathbf{c}_t=f_t\circ{\mathbf{c}_{t-1}}+i_t\circ{\mathbf{\tilde{c}}_t}\qquad\quad(式4)$$

符号O表示按元素乘。下图是$c_t$的计算：

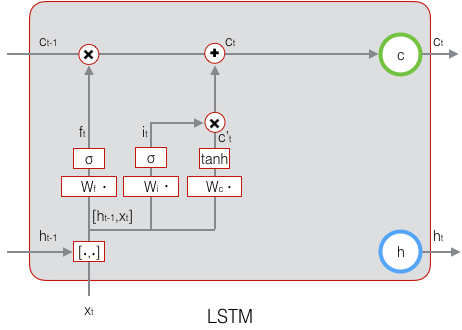
这样，我们就把LSTM关于当前的记忆$\tilde{c}_t$和长期的记忆$c_{t-1}$组合在一起，形成了新的单元状态$c_t$。由于遗忘门的控制，它可以保存很久很久之前的信息，由于输入门的控制，它又可以避免当前无关紧要的内容进入记忆。下面，我们要看看输出门，它控制了长期记忆对当前输出的影响：

$$\mathbf{o}_t=\sigma(W_o\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_o)\qquad\quad(式5)$$

下面表示输出门的计算：

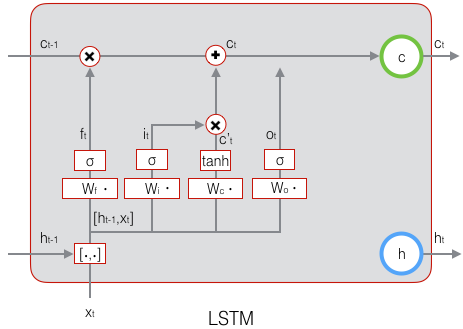
LSTM最终的输出，是由输出门和单元状态共同确定的：

$$\mathbf{h}_t=\mathbf{o}_t\circ \tanh(\mathbf{c}_t)\qquad\quad(式6)$$

下图表示LSTM最终输出的计算：

式1到式6就是LSTM前向计算的全部公式。至此，我们就把LSTM前向计算讲完了。

长短时记忆网络的训练

LSTM训练算法框架

LSTM的训练算法仍然是反向传播算法，对于这个算法，我们已经非常熟悉了。主要有下面三个步骤：

1、前向计算每个神经元的输出值，对于LSTM来说，即$f_t$、$i_t$、$c_t$、$o_t$、$h_t$五个向量的值。计算方法已经在上一节中描述过了。

2、反向计算每个神经元的误差项$\delta$值。与循环神经网络一样，LSTM误差项的反向传播也是包括两个方向：一个是沿时间的反向传播，即从当前t时刻开始，计算每个时刻的误差项；一个是将误差项向上一层传播。

3、根据相应的误差项，计算每个权重的梯度。

关于公式和符号的说明

我们设定gate的激活函数为sigmoid函数，输出的激活函数为tanh函数。他们的导数分别为：