zzuli1728(数学期望，组合数)

1728: 社交网络

Time Limit: 2 Sec  Memory Limit: 128 MB
Submit: 232  Solved: 64

SubmitStatusWeb Board

Description

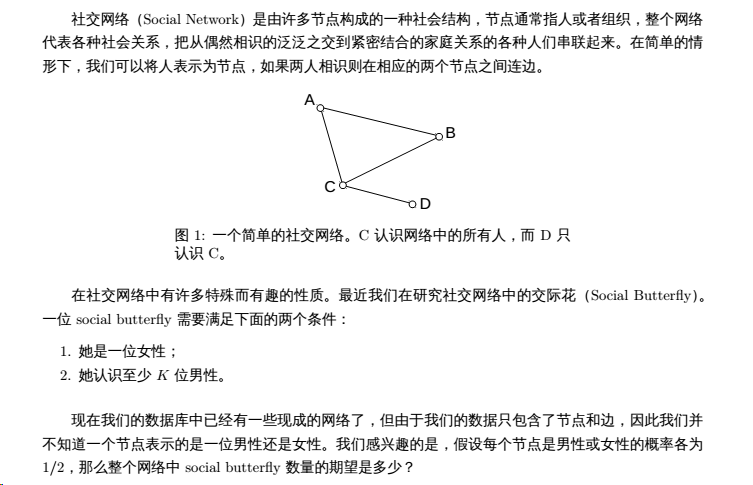
Input

Output

Sample Input

2
2 1
0 1
1 0
3 1
0 1 1
1 0 1
1 1 0

Sample Output

0.500
1.125 

 

看见数学，一如既往懵逼，不过后来在纸上慢慢也找到解法了算是。

首先每个人都有若干个有关系的人(设为n)存在，要想这个人是交际花的话，此人必定是女的所以E=1*0.5；

又因为必须要认识k个男的的要求，所以n>=k，接着就是计算可能性有多少种，假设j表示n个人中男的数量，显然所有的可能性是：（j=k,j=k+1,j=k+2......j=n)

接着问题就来了n个人中j个男人的概率是多少，显然要用到组合数，因为n最大30大大超过了LL的范围所以不能直接计算只能通过打表存下C[30][30]内的组合数！

由于男女的概率对半分所以直接乘上0.5^n即可表示这些人组成这些性别的概率；

 

学习到了组合数的打表计算，和计算复杂概率

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#define CIN(a) scanf("%d",&a)
using namespace std;
int G[35];
long long C[32][32];
void init()
{
int i,j;
for(i=1;i<=31;++i) C[i][0]=1,C[i][1]=1,C[i][i]=1;
for(i=1;i<=31;++i)
for(j=1;j<=i;++j)
C[i][j]=C[i][j-1]*(i-j+1)/j;
}
double POW(double a,int b)
{
double s=1.00;
for(int i=1;i<=b;++i) s=s*a;
return s;
}
int main()
{init();
int t,i,j,n,k;
CIN(t);
while(t--){int b;memset(G,0,sizeof(G));
double P=0,E=0;
CIN(n),CIN(k);
for(i=1;i<=n;++i)
for(j=1;j<=n;++j) {CIN(b);
if(b==1) G[i]++;
}
for(i=1;i<=n;++i)
for(j=k;j<=G[i];++j){
E+=0.5*(C[G[i]][j]*POW(0.5,G[i]));        //n个人中有j个人是男的时第i号人是交际花的概率（由于只是一个人，此值也表示期望）
}
printf("%.3f\n",E);
}
return 0;
}