循环神经网络(RNN)模型与前向反向传播算法

　　　　在前面我们讲到了DNN，以及DNN的特例CNN的模型和前向反向传播算法，这些算法都是前向反馈的，模型的输出和模型本身没有关联关系。今天我们就讨论另一类输出和模型间有反馈的神经网络：循环神经网络(Recurrent Neural Networks ，以下简称RNN)，它广泛的用于自然语言处理中的语音识别，手写书别以及机器翻译等领域。

1. RNN概述

　　　　在前面讲到的DNN和CNN中，训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决，就是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。

　　　　而对于这类问题，RNN则比较的擅长。那么RNN是怎么做到的呢？RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引$\tau$的。对于这其中的任意序列索引号$t$,它对应的输入是对应的样本序列中的$x^{(t)}$。而模型在序列索引号$t$位置的隐藏状态$h^{(t)}$，则由$x^{(t)}$和在$t-1$位置的隐藏状态$h^{(t-1)}$共同决定。在任意序列索引号$t$，我们也有对应的模型预测输出$o^{(t)}$。通过预测输出$o^{(t)}$和训练序列真实输出$y^{(t)}$,以及损失函数$L^{(t)}$，我们就可以用DNN类似的方法来训练模型，接着用来预测测试序列中的一些位置的输出。

　　　　下面我们来看看RNN的模型。

2. RNN模型

　　　　RNN模型有比较多的变种，这里介绍最主流的RNN模型结构如下：

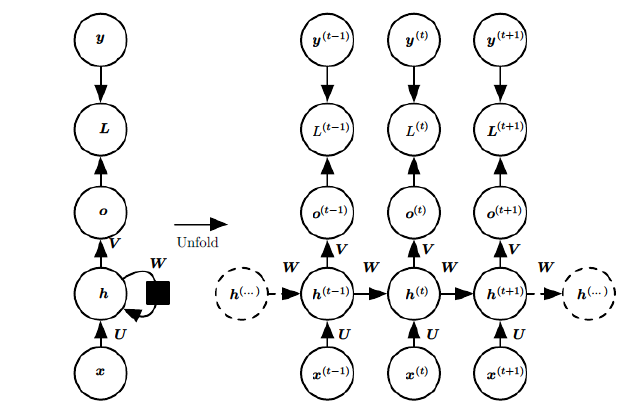
　　　　上图中左边是RNN模型没有按时间展开的图，如果按时间序列展开，则是上图中的右边部分。我们重点观察右边部分的图。

　　　　这幅图描述了在序列索引号$t$附近RNN的模型。其中：

　　　　1）$x^{(t)}$代表在序列索引号$t$时训练样本的输入。同样的，$x^{(t-1)}$和$x^{(t+1)}$代表在序列索引号$t-1$和$t+1$时训练样本的输入。

　　　　2）$h^{(t)}$代表在序列索引号$t$时模型的隐藏状态。$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$共同决定。

　　　　3）$o^{(t)}$代表在序列索引号$t$时模型的输出。$o^{(t)}$只由模型当前的隐藏状态$h^{(t)}$决定。

　　　　4）$L^{(t)}$代表在序列索引号$t$时模型的损失函数。

　　　　5）$y^{(t)}$代表在序列索引号$t$时训练样本序列的真实输出。

　　　　6）$U,W,V$这三个矩阵是我们的模型的线性关系参数，它在整个RNN网络中是共享的，这点和DNN很不相同。 也正因为是共享了，它体现了RNN的模型的“循环反馈”的思想。　　

3. RNN前向传播算法

　　　　有了上面的模型，RNN的前向传播算法就很容易得到了。

　　　　对于任意一个序列索引号$t$，我们隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$得到：$$h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b )$$

　　　　其中$\sigma$为RNN的激活函数，一般为$tanh$, $b$为线性关系的偏倚。

　　　　序列索引号$t$时模型的输出$o^{(t)}$的表达式比较简单：$$o^{(t)} = Vh^{(t)} +c $$

　　　　在最终在序列索引号$t$时我们的预测输出为:$$\hat{y}^{(t)} = \sigma(o^{(t)})$$

　　　　通常由于RNN是识别类的分类模型，所以上面这个激活函数一般是softmax。

　　　　通过损失函数$L^{(t)}$，比如对数似然损失函数，我们可以量化模型在当前位置的损失，即$\hat{y}^{(t)}$和$y^{(t)}$的差距。

4. RNN反向传播算法推导

　　　　有了RNN前向传播算法的基础，就容易推导出RNN反向传播算法的流程了。RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数$U,W,V,b,c$。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的$U,W,V,b,c$在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。

　　　　为了简化描述，这里的损失函数我们为对数损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。

　　　　对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失$L$为：$$L = \sum\limits_{t=1}^{\tau}L^{(t)}$$

　　　　其中$V,c,$的梯度计算是比较简单的：$$\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}$$$$\frac{\partial L}{\partial V} =\sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T$$

　　　　但是$W,U,b$的梯度计算就比较的复杂了。为啥呢？比如我们看看$W$在某一序列位置t的梯度损失如下：$$\frac{\partial L^{(t)}}{\partial W} = \frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial W}=  (\hat{y}^{(t)} - y^{(t)}) V^T\frac{\partial h^{(t)}}{\partial W}$$

　　　　前面的两部分部分偏导数都好计算，难点在$\frac{\partial h^{(t)}}{\partial W}$。看似$h^{(t)} =   \sigma(Ux^{(t)} + Wh^{(t-1)} +b ) $，这样$\frac{\partial h^{(t)}}{\partial W}$的结果就是激活函数的导数乘以系数$h^{(t-1)}$转置。但是问题是：$h^{(t-1)} = \sigma(Ux^{(t-1)} + Wh^{(t-2)}+b )$，也就是$h^{(t-1)}$中也含有$W$,我们不能简单的把$h^{(t-1)}$当做系数，要计算$\frac{\partial h^{(t)}}{\partial h^{(t-1)}}$的依赖关系。

　　　　也就是说，在反向传播时，在在某一序列位置t的梯度损失由当前位置的损失和序列索引位置$t+1$时的梯度损失两部分共同决定。对于$W$在某一序列位置t的梯度损失需要反向传播一步步的计算。我们定义序列索引$t$位置的隐藏状态的梯度为：$$\delta^{(t)} = \frac{\partial L^{(t)}}{\partial h^{(t)}}$$

　　　　这样我们可以像DNN一样从$\delta^{(t+1)} $递推$\delta^{(t)}$ 。$$\delta^{(t)} =\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L^{(t)}}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-(h^{(t)})^2)$$

　　　　有了$\delta^{(t+1)} $,计算$W,U,b$就容易了，这里给出$W,U,b$的梯度计算表达式：$$\frac{\partial L}{\partial W} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial W} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(h^{(t-1)})^T$$$$\frac{\partial L}{\partial b} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial b} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}$$$$\frac{\partial L}{\partial U} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial U} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(x^{(t)})^T$$

　　　　除了梯度表达式不同，RNN的反向传播算法和DNN区别不大，因此这里就不再重复总结了。

5. RNN小结

　　　　上面总结了通用的RNN模型和前向反向传播算法。当然，有些RNN模型会有些不同，自然前向反向传播的公式会有些不一样，但是原理基本类似。

　　　　RNN虽然理论上可以很漂亮的解决序列数据的训练，但是它也像DNN一样有梯度消失时的问题，当序列很长的时候问题尤其严重。因此，上面的RNN模型一般不能直接用于应用领域。在语音识别，手写书别以及机器翻译等NLP领域实际应用比较广泛的是基于RNN模型的一个特例LSTM，下一篇我们就来讨论LSTM模型。

（欢迎转载，转载请注明出处。欢迎沟通交流： pinard.liu@ericsson.com）

参考资料：

1） Neural Networks and Deep Learning by By Michael Nielsen

2） Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville

3） UFLDL Tutorial

4）CS231n Convolutional Neural Networks for Visual Recognition, Stanford