算法录 之 BFS和DFS

　　说一下BFS和DFS，这是个比较重要的概念，是很多很多算法的基础。

　　不过在说这个之前需要先说一下图和树，当然这里的图不是自拍的图片了，树也不是能结苹果的树了。这里要说的是图论和数学里面的概念。

　　

　　以上概念来自百度百科。

　　数学里面的图就是许多的点和许多的边把这些点连了起来，具体每个点放在那里没啥关系，重点是他们之间的连接关系。

　　一个图长得就像是下面这样：

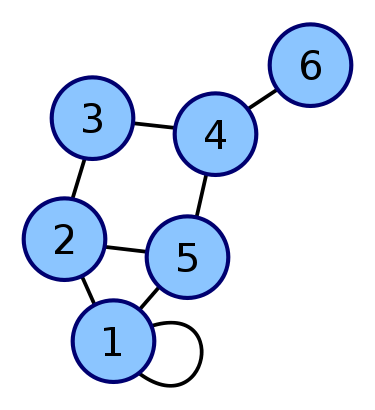
　　这个图有6个点，8条边，其中有一条是自己连接自己的。

　　然后图的话有有向图，无向图等等，还有很多很多分类，比如二分图等等，可以百度百科或者维基看一下就差不多明白了。

　　然后树的话其实也是图，但是比较特殊而已，他有N个点，N-1条边，而且这N个点是互相连通的，那么这个图就能画成一颗树一样的样子。

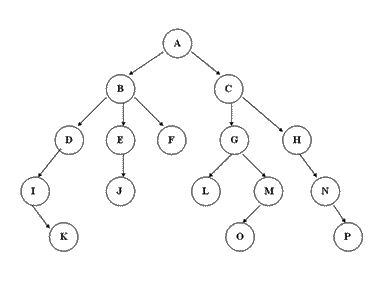
　　倒过来看就很像一棵树。

　　然后下面要说的是BFS和DFS，这两个是一个缩写，全称是 BFS：Breadth-First-Search，宽度优先搜索；DFS：Depth-first search，深度优先搜索。

　　都是一种搜索，只不过搜索的方法不一样而已。

　　先说说搜索，顾名思义，搜索就是。。。搜索。对于一个图来说，搜索就是从某个点开始，不停的搜索与他相连的所有的点，然后以此接连下去，直到所有的点都被搜索到了。

　　然后BFS的话就是宽度优先。

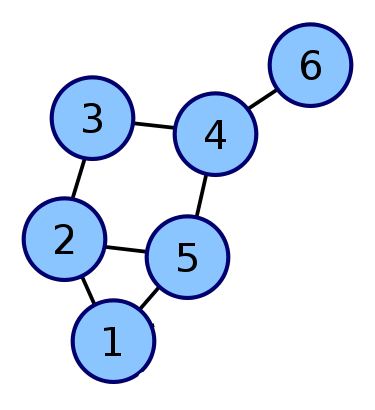
　　比如这个图，如果从1开始进行搜索的话，BFS的步骤就是，先搜索所有和1相连的，也就是2和5被找到了，然后再从2开始搜索和他相连的，也就是3被找到了，然后从5搜，也就是4被找到了，然后从3开始搜索，4被找到了，但是4之前已经被5找到了，所以忽略掉就行。然后3开始搜索，忽略4所以啥都没搜到，然后从4开始，6被找到了。。。

　　就是这样，这就是BFS。。。

　　说完DFS比较一下两个的区别可能会比较好理解。

　　DFS的话从1开始，先找到其中一个相连的，2被找到了，然后直接开始从2开始搜索，3被找到了，然后从3开始搜索，4被找到了，然后从4开始搜索，5被找到了，然后从5开始搜索，忽略已经找到的所以啥都没找到。然后没路可走了，回到前面去再走另一条路，从4开始，6被找到了，然后又没路可走了，然后再回去前面4，然后没路了 ，回去前面3，然后一直这样。。。

　　DFS 就是像走迷宫一样一条路走到头直到走不通才回到前一个换一条路。。。就是这样。。。

　　DFS和BFS主要是运用于对于图和树的搜索，但是绝大部分问题模型都是可以建模变成一个图或者树的，所以差不多不少问题都会涉及到这两个。

　　现在知道了这个东西的实现的步骤了。下面就要说一下怎么用代码来实现他。

　　先说图吧，对于每个点来说就是标号1,2,3。。。。N就好，表示有N个结点，一般题目也已经标好号了。

　　然后边的话一般会就是 u，v 这样表示有一条边连接u点和v点。

　　存储一个图的边有三种方法：

　　首先说一下存图就是对于每个点u，记录他能到的所有点就行了。。。

　　邻接矩阵：

　　直接开一个N×N的二维数组E，然后 E[i][j] 为1的时候表示 i 和 j 之间有一条边，0的时候就没有。

　　这样很方便简单，但是有几个缺陷，首先是效率问题，超过1000个点一般不管是空间还是时间都不允许了。然后就是如果从 3 到 5 有两条边的话，就没法表示了。。。

　　所以一般很少用了现在，当然有些算法还是会用到的。

int E[][];

E[][]=;
E[][]=;

　　邻接链表：

　　使用链表的方式保存一个结点的所有边，就是每个点都有一个链表。

　　当然写个链表很麻烦，所以一般是用vector来替代。就像是下面这样。

vector <int> E[];

E[].push_back() // 有一条从3到6的边。

　　具体vector怎么用自行学习

　　前向星：

　　这个名字实在逼格太高，而且很好用效率也高，所以我一直都用这种方式来存图。

　　他和链表几乎没什么区别，就是每次添加新的边的时候往开头加，而不是往最后加。

具体就像是下面这样：

struct Edge
{
    int to,next;
};

Edge E[];            // 总共不超过1000条边。
int head[],Ecou;        // 不超过100个点。

void init()                // 初始化。
{
    memset(head,-,sizeof(head));
    Ecou=;
}

void addEdge(int u,int v)    // 增加边 u，v。
{
    E[Ecou].to=v;
    E[Ecou].next=head[u];
    head[u]=Ecou++;
}

　　具体的代码可以慢慢理解，而且刚开始的话用前面两种也可以。

　　然后说说BFS和DFS怎么写。

　　首先BFS的话需要一个队列这种数据结构来保存，队列在另一篇有说。

　　因为每次找到和u相连的之后要一个个找这些点，符合先进先出。

代码如下：（采用第二种存图方式。）

bool vis[];            // 记录已经走过的点，防止重复访问。

void BFS(int root,int N)        // N个点的图，从root点开始搜索。
{
    queue <int> que;

    memset(vis,,sizeof(vis));    // 初始化。
    vis[root]=;
    que.push(root);

    int u,len;

    while(!que.empty())
    {
        u=que.front();
        que.pop();

        len=E[u].size();
        for(int i=;i<len;++i)        // 找到和u相连的所有点，存在一个vector里面。
            if(vis[E[u][i]]==)
            {
                vis[E[u][i]]=;
                que.push(E[u][i]);
            }
    }
}

　　十分建议手算模拟一下这个算法，对于步骤有一个清晰的认识。

然后是DFS：需要一个栈，因为每次都是搜到之后不停的往下搜，符合先进先出。但是一般来说不用栈，而是直接通过函数的递归就行了。

bool vis[];
int N;

void DFS(int u)
{
    int len;

    vis[u]=;
    len=E[u].size();

    for(int i=;i<len;++i)
        if(vis[E[u][i]]==)
            DFS(E[u][i]);
}

　　差不多就是这样，也建议好好模拟一下。

　　至于这两个的用途，其实在一定程度上是可以相互转化的，但是有些需要各自的特性的话就不行了。

　　DFS主要的特性是深度优先，总是不停的往下找，走到没路才罢休。

　　BFS则是从root开始扩展，每一层都是精密的搜索完整了才下一个。