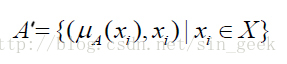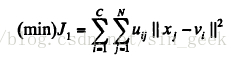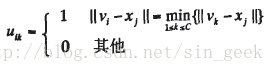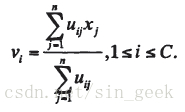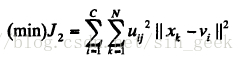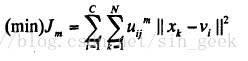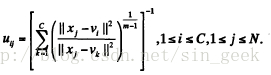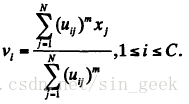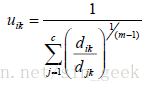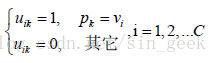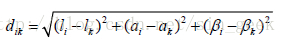模糊聚类算法（FCM）

伴随着模糊集理论的形成、发展和深化，RusPini率先提出模糊划分的概念。以此为起点和基础，模糊聚类理论和方法迅速蓬勃发展起来。针对不同的应用，人们提出了很多模糊聚类算法，比较典型的有基于相似性关系和模糊关系的方法、基于模糊等价关系的传递闭包方法、基于模糊图论的最大支撑树方法，以及基于数据集的凸分解、动态规划和难以辨别关系等方法。然而，上述方法均不能适用于大数据量的情况，难以满足实时性要求较高的场合，因此实际应用并不广泛。

模糊聚类分析按照聚类过程的不同大致可以分为三大类：

(1)基于模糊关系的分类法：其中包括谱系聚类算法(又称系统聚类法)、基于等价关系的聚类算法、基于相似关系的聚类算法和图论聚类算法等等。它是研究比较早的一种方法，但是由于它不能适用于大数据量的情况，所以在实际中的应用并不广泛。

(2)基于目标函数的模糊聚类算法：该方法把聚类分析归结成一个带约束的非线性规划问题，通过优化求解获得数据集的最优模糊划分和聚类。该方法设计简单、解决问题的范围广，还可以转化为优化问题而借助经典数学的非线性规划理论求解，并易于计算机实现。因此，随着计算机的应用和发展，基于目标函数的模糊聚类算法成为新的研究热点。

(3)基于神经网络的模糊聚类算法：它是兴起比较晚的一种算法，主要是采用竞争学习算法来指导网络的聚类过程。

在介绍算法之前，先介绍下模糊集合的知识。

HCM聚类算法

首先说明隶属度函数的概念。隶属度函数是表示一个对象x 隶属于集合A 的程度的函数，通常记做μA(x)，其自变量范围是所有可能属于集合A 的对象（即集合A 所在空间中的所有点），取值范围是[0,1]，即0<=μA(x)，μA(x)<=1。μA(x)=1 表示x 完全隶属于集合A，相当于传统集合概念上的x∈A。一个定义在空间X={x}上的隶属度函数就定义了一个模糊集合A，或者叫定义在论域X={x}上的模糊子集A’。对于有限个对象x1，x2，……，xn 模糊集合A’可以表示为：

有了模糊集合的概念，一个元素隶属于模糊集合就不是硬性的了，在聚类的问题中，可以把聚类生成的簇看成模糊集合，因此，每个样本点隶属于簇的隶属度就是[0，1]区间里面的值。

再接下来要讲FCM算法不得不先讲一下HCM算法

硬C-均值(HCM)算法是实现数据集J硬C划分的经典算法之一，也是最受欢迎的算法之一。它能够把数据集X分成C个超椭球结构的聚类。HCM算法把传统的聚类问题归结为如下的非线性数学规划问题：

其中U=(u_ij)_cxn为硬C-划分矩阵，V=(v1，v2，，，vc)为C个聚类中心，||·||代码欧式距离。

HCM算法的具体流程如下：

初始化：指定聚类类别数C，2<=C<=n，n是数据个数，设定迭代停止阈值Ɛ，初始化聚类中心V0，设置迭代计数器b=0；

步骤一：根据下面的公式计算或更新划分矩阵U

步骤二：根据下面公式更新聚类中心V（b+1）

步骤三：如果||Vb – V(b+1)||< Ɛ，则算法停止并输出划分矩阵和聚类中心V，否则令b=b+1，转向执行步骤一

FCM聚类算法

Dunn按照RusPini定义的模糊划分的概念，把HCM算法扩展到模糊划分领域。Dunn对每个样本与每个聚类中心的距离用其隶属度平方加权，从而把类内误差平方和目标函数J1扩展为类内加权误差平方和函数J2：

Bezdek又将Dunn的目标函数推广为更普遍的形式，给出了基于目标函数的模糊聚类更一般的描述。

其中，m∈[1,+∞)称为加权指数，又称作平滑参数。尽管从数学角度看，m的出现不自然，但如果不对隶属度加权，从HCM算法到FCM算法的推广将是无效的。

FCM算法的具体流程如下：

初始化：指定聚类类别数C，2<=C<=n，n是数据个数，设定迭代停止阈值Ɛ，初始化聚类中心V0，设置迭代计数器b=0；

步骤一：根据下面的公式计算或更新划分矩阵U

步骤二：根据下面公式更新聚类中心V（b+1）

步骤三：如果||Vb – V(b+1)||< Ɛ，则算法停止并输出划分矩阵和聚类中心V，否则令b=b+1，转向执行步骤一

FCM算法流程图

FCM算法是目前比较流行的一种模糊聚类算法，究其原因大致有以下几个方面：首先，模糊C—均值泛函J_m仍是传统硬C一均值泛函J₁的自然推广；硬C一均值泛函J₁是一个应用十分广泛的聚类准则，对其在理论上的研究己经相当完善，这就为J_m的研究提供了良好的条件；数学上看，J_m与R^S的希尔伯特空间结构(正交投影和均方逼近理论)有密切的关系，因此比其它泛函有更深厚的数学基础；最后，也是最重要的是该目标函数不仅在许多领域获得了非常成功的应用，而且以FCM算法为基础，人们提出的基于其它原型的模糊聚类算法，形成了一大批FCM类型的算法：如模糊C一线(FCL)、模糊C一面(FCP)等聚类算法，分别实现了对呈线状、超平面状结构模式子集(或聚类)的检测。

FCM算法应用到颜色迁移中

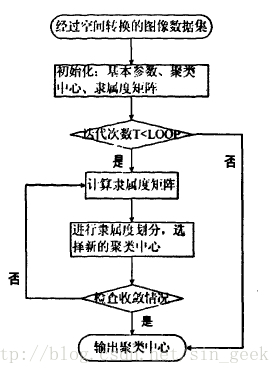
钱小燕等人将聚类算法应用到色彩迁移中，提出了一种基于图像模糊颜色聚类的自适应色彩迁移算法。该算法首先将源图像和目标图像分别转换到lαβ颜色空间：利用FCM 算法把源图像和目标图像划分为具有不同颜色特征的聚类，然后分析图像中的颜色特征：分别算出每个域的匹配权值，对每个目标图像的匹配权值，从源图像中选取一个最接近域作为最佳匹配域；最后根据目标图像各聚类域与源图像中的匹配域之间的关系，引入隶属度因子，两个域的处理结果分别进行加权平均，获得色彩迁移结果。使用FCM的思想对图像进行聚类域划分的思路是：设准备处理图像I的大小是S×H，即对颜色聚类颜色分析的个数是N，N = S×H，则图像I可表示成集合，I={p1 ,p2 ...,pn }。图像被分为c类，每个类的聚类中心为V={v1,v2 ...,vc }，用u_ik表示像素p_k隶属于聚类中心Vi的隶属度，定义图像的隶属度矩阵U。具体算法如下：

步骤一：把源图像和目标图像分别从RGB转换到lαβ空间。

步骤二：确定待处理图像聚类域个数c，然后初始化聚类中心。假设加权指数m=2，设定处理的最大迭代次数为50。

步骤三：当迭代次数T 小于50 时，根据初始化聚类中心计算隶属度矩阵。如果p_k≠vi,则对于所有的vi ( i=1,2,...,C )，利用下式计算隶属度矩阵。

其中，i =1,2,...C； j =1,2,...N

如果，p_k=vi,，k =1,2,...N则

其中，d_ik为第k个元素到第i 个聚类中心的距离，定义在lαβ下的欧式距离。

步骤四：对图像聚类划分。图像的隶属度矩阵中，从每列选择隶属度最大的点作为相对应点的归属域，并重新计算聚类中心。

步骤五：对收敛情况进行检查。若||Vi – V’i||<Σ，则立即停止迭代；否则一直迭代计算步骤三与步骤四。

步骤六：对聚类域进行匹配。使用FCM 后，对每一个聚类域分别设置一个匹配权值参数w，当目标图像是灰度图像时，w为聚类域的亮度均值；当目标图像为彩色图像时，w 是聚类域3 个通道标准差的加权平均值。

步骤七：色彩迁移。为了保持通用性，假定目标图像中元素pi的归属域与源图像中聚类域h 是匹配域，利用下式获得各个通道的新值：

FCM算法效果图

1. BOOL TranFCM(LPBYTE lpDIBBits, LONG lmageWidth, LONG lmageHeight,LPBYTE lpDIBBits2, LONG lmageWidth2, LONG lmageHeight2,LPBYTE lpDIBBits3)
2. {
3. int classnum=2;
4. int m=2;
5. int i,j,k,nindex;
6. double l,a,b;
7. double* belong=new double[lmageWidth*lmageHeight*classnum];
8. double* belong2=new double[lmageWidth2*lmageHeight2*classnum];
9. double* center=new double[classnum*3];
10. double* center2=new double[classnum*3];
11. int* clustermap=new int[classnum];
12. double suml,suma,sumb;
13. FCMCluster(lpDIBBits,lmageWidth,lmageHeight,belong,center,classnum,m);
14. FCMCluster(lpDIBBits2,lmageWidth2,lmageHeight2,belong2,center2,classnum,m);
15. double* vl=new double[classnum];
16. double* va=new double[classnum];
17. double* vb=new double[classnum];
18. double* vl2=new double[classnum];
19. double* va2=new double[classnum];
20. double* vb2=new double[classnum];
21. for(i=0;i<classnum;i++)
22. {
23. BYTE distance=255;
24. int map=-1;
25. BYTE r,g,b,r2,g2,b2;
26. for(j=0;j<classnum;j++)
27. {
28. LabToRgb(center[i*3+0],center[i*3+1],center[i*3+2],r,g,b);
29. LabToRgb(center2[j*3+0],center2[j*3+1],center2[j*3+2],r2,g2,b2);
30. BYTE dis=abs(RgbToGray(r,g,b)-RgbToGray(r2,g2,b2));
31. if (distance>dis) {distance=dis;map=j;}
32. }
33. clustermap[i]=map;
34. }
35. //TranColor(belong,belong2,center,center2);
36. //求各聚类域的标准差
37. //求结果图像的lab
38. for(j = 0;j <lmageHeight; j++)
39. {
40. for(i = 0; i <lmageWidth; i++)
41. {
42. nindex=((lmageHeight-j-1)*lmageWidth+i);
43. suml=suma=sumb=0;
44. RgbToLab(lpDIBBits[nindex*3+2],lpDIBBits[nindex*3+1],lpDIBBits[nindex*3+0],l,a,b);
45. for(k=0;k<classnum;k++)
46. {
47. suml += belong[lmageWidth*lmageHeight*k+nindex]*center2[clustermap[k]*3+0];
48. suma += belong[lmageWidth*lmageHeight*k+nindex]*center2[clustermap[k]*3+1];
49. sumb += belong[lmageWidth*lmageHeight*k+nindex]*center2[clustermap[k]*3+2];
50. }
51. LabToRgb(l,suma,sumb,lpDIBBits3[nindex*3+2],lpDIBBits3[nindex*3+1],lpDIBBits3[nindex*3+0]);
52. }
53. }
54. return TRUE;
55. }

1. BOOL FCMCluster(LPBYTE lpDIBBits, LONG lmageWidth, LONG lmageHeight,double* belong,double* center,int classnum,int m)
2. {
3. int i,j,l,nindex;//循环控制变量
4. int k=0;
5. int LOOP=500;
6. double* center2=new double[classnum*3];//聚类中心
7. long x,y;//随机确定聚类中心坐标
8. long* num=new long[classnum];//每个类的像素个数
9. double* lpImageLab = new  double[lmageWidth*lmageHeight*3];
10. double sumu,suml,suma,sumb;
11. //初始化聚类中心
12. for(i=0;i<classnum;i++)
13. {
14. x=rand()%lmageWidth;
15. y=rand()%lmageHeight;
16. nindex=((lmageHeight-y-1)*lmageWidth+x);
17. RgbToLab(lpDIBBits[nindex*3+2],lpDIBBits[nindex*3+1],lpDIBBits[nindex*3+0],center[i*3+0],center[i*3+1],center[i*3+2]);
18. for(j=0;j<i;j++)
19. {
20. double dis=DistanceLab(center[i*3+0],center[i*3+1],center[i*3+2],center[j*3+0],center[j*3+1],center[j*3+2]);
21. if(dis<0.2) {i--;break;}//限值公式 暂取限值为1待优化 对初始化聚类中心的选择非常关键
22. }
23. }
24. //计算隶属度矩阵、更新聚类中心、直至前后聚类中心距离小于限值e暂定0.1待优化
25. while(k!=classnum && LOOP--)//限值公式
26. {
27. //计算隶属度矩阵
28. for(j = 0;j <lmageHeight; j++)
29. {
30. for(i = 0; i <lmageWidth; i++)
31. {
32. nindex=((lmageHeight-j-1)*lmageWidth+i);
33. RgbToLab(lpDIBBits[nindex*3+2],lpDIBBits[nindex*3+1],lpDIBBits[nindex*3+0],
34. lpImageLab[nindex*3+0],lpImageLab[nindex*3+1],lpImageLab[nindex*3+2]);
35. //means_Assign();
36. double blg=-1;//隶属度
37. for(k=0;k<classnum;k++)
38. {
39. sumu=0;
40. double dis1=DistanceLab(lpImageLab[nindex*3+0],lpImageLab[nindex*3+1],lpImageLab[nindex*3+2],center[k*3+0],center[k*3+1],center[k*3+2]);
41. if (dis1==0) {belong[lmageWidth*lmageHeight*k+nindex]=1;continue;}
42. for(l=0;l<classnum;l++)
43. {
44. double dis2=DistanceLab(lpImageLab[nindex*3+0],lpImageLab[nindex*3+1],lpImageLab[nindex*3+2],center[l*3+0],center[l*3+1],center[l*3+2]);
45. if (dis2==0) break;
46. sumu+=pow((dis1*dis1)/(dis2*dis2),1.0/(m-1));
47. }
48. if (l!=classnum) {belong[lmageWidth*lmageHeight*k+nindex]=0;continue;}
49. belong[lmageWidth*lmageHeight*k+nindex]=1/sumu;
50. }
51. }
52. }
53. //更新聚类中心
54. for(k=0;k<classnum;k++)
55. {
56. suml=suma=sumb=sumu=0;
57. for(j = 0;j <lmageHeight; j++)
58. {
59. for(i = 0; i <lmageWidth; i++)
60. {
61. nindex=((lmageHeight-j-1)*lmageWidth+i);
62. suml+=pow(belong[lmageWidth*lmageHeight*k+nindex],m)*lpImageLab[nindex*3+0];
63. suma+=pow(belong[lmageWidth*lmageHeight*k+nindex],m)*lpImageLab[nindex*3+1];
64. sumb+=pow(belong[lmageWidth*lmageHeight*k+nindex],m)*lpImageLab[nindex*3+2];
65. sumu+=pow(belong[lmageWidth*lmageHeight*k+nindex],m);
66. }
67. }
68. center2[k*3+0]=suml/sumu;
69. center2[k*3+1]=suma/sumu;
70. center2[k*3+2]=sumb/sumu;
71. }
72. //判断循环终止条件
73. for(k=0;k<classnum;k++)
74. {
75. if(DistanceLab(center[k*3+0],center[k*3+1],center[k*3+2],center2[k*3+0],center2[k*3+1],center2[k*3+2])>0.1) break;//限值e暂定0.1待优化
76. }
77. for(i=0;i<classnum*3;i++)
78. {
79. center[i]=center2[i];
80. }
81. }
82. return TRUE;
83. }

1. double DistanceLab(double l1,double a1,double b1,double l2,double a2,double b2)
2. {
3. double lx=l1-l2;
4. double ax=a1-a2;
5. double bx=b1-b2;
6. if (lx<0) lx=-lx;
7. if (ax<0) ax=-ax;
8. if (bx<0) bx=-bx;
9. return lx+ax+bx;
10. }

代码链接

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/lyh03601/article/details/22896197