Levenshtein距离

　　Levenshtein Distance，又称Edit Distance，在自然语言处理中有着广泛的应用。Levenshtein  Distance 指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。编辑操作包括：1）删除一个字符；2）插入一个字符；3）替换一个字符

　　Example:

　　两个字符串a = "kitten", b = "ssitting"，编辑过程如下：

• kitten → sitten (substitution of "s" for "k")
• sitten → sittin (substitution of "i" for "e")
• sittin → sitting (insertion of "g" at the end).

　　因此，a与b之间的编辑距离等于3。

　　解决方案：动态规划

　　1）描述最优解结构，寻找最优子结构

　　a = {x₁, x₂..x_i}与字符串b = {y₁, y₂...y_j}之间的最小编辑次数lev_a,b(i, j)。

• 　如果x_i = y_j，lev_a,b(i, j) = lev_a,b(i-1, j-1)
• 　如果x_i ≠ y_j，lev_a,b(i, j)将是以下三种情况中，编辑次数最少的一个

　　(1) 替换x_i ，让x_i 替换y_j，编辑距离lev_a,b(i, j) =  lev_a,b(i-1, j-1) + 1

　　　　　　(2) 在a中的第i个位置，插入新字符x让字符x = y_j，lev_a,b(i, j) =  lev_a,b(i, j-1) + 1

　　　　　　(3) 在a中的第i个位置， 删除入字符x_i ，lev_a,b(i, j) =  lev_a,b(i-1, j) + 1

　　2）递归定义最优解

　　有了上面的分析，递归表达式可以容易的推导出来：

　　

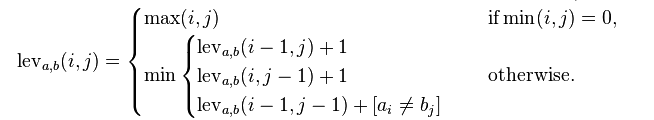
　　3）自底向上的实现

　　

#include <iostream>

using namespace std;

/************************************************************************/
/*
 *  a: 源字符串
 *  b: 目的字符串
 *  m: 源字符串长度
 *  n: 目的字符串的长度
/************************************************************************/
int lev_distance(const char* a, const char* b, int m, int n)
{
    int* pre_col = new int[n+];
    int* cur_col = new int[n+];

    for (int i = ; i != n+; i++)
    {
        pre_col[i] = i;
    }

    for (int i = ; i != m; i++)
    {
        cur_col[] = i + ;
        for (int j = ; j < n; j++)
        {
            cur_col[j+] = min(min( + cur_col[j],  + pre_col[j+]),
                                        pre_col[j] + (a[i] == b[j] ?  : ));
        }
        swap(pre_col, cur_col);
    }

    return pre_col[n];
}

int main()
{
    char a[] = "kitten";
    char b[] = "sitting";

    int dist = lev_distance(a, b, sizeof(a)-, sizeof(b)-);

    cout<<"levenshtein distance:"<<dist<<endl;

    system("pause");
    return ;
}

　　正常的动态规划算法需要记录表格大小是len(a) * len(b)，当字符串长度较长的情况下，将需要很大的存储空间，上面的算法针对这种情况做了一个小的改进：lev(i, j)仅依赖于表格中的三个位置，左边，上方，左上方，因此只要保留当前列与左边一列就可以求出lev(i, j)的值了。