最短路径——floyd(多源最短路径)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <malloc.h> using namespace std; const int VERTEX_NUM = 20;
const int INFINITY = 0x7fffffff; bool vis[VERTEX_NUM];
int dist[VERTEX_NUM][VERTEX_NUM]; class Graph {
public:
int vexNum;
int edgeNum;
int vex[VERTEX_NUM];
int arc[VERTEX_NUM][VERTEX_NUM];
}; void createGraph(Graph &G)
{
cout << "please input vexNum and edgeNum: ";
cin >> G.vexNum >> G.edgeNum;
for (int i = 0; i != G.vexNum; ++i) {
cout << "please input no" << i+1 << " vertex: ";
cin >> G.vex[i]; // 自定义顶点序号
}
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (i == j) G.arc[i][j] = 0;
else G.arc[i][j] = INFINITY;
}
}
for (int k = 0; k != G.edgeNum; ++k) {
cout << "please input the vertex of edge(vi, vj) and weight: ";
int i, j, w;
cin >> i >> j >> w;
G.arc[i][j] = w;
G.arc[j][i] = G.arc[i][j];
}
} // Floyd算法
void floyd(Graph &G)
{
memset(dist, INFINITY, VERTEX_NUM);
for (int k = 0; k != G.vexNum; ++k) {
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (G.arc[i][j] > G.arc[i][k] + G.arc[k][j] && G.arc[i][k] < INFINITY && G.arc[k][j] < INFINITY) {
G.arc[i][j] = G.arc[i][k] + G.arc[k][j];
}
}
}
}
} int main()
{
Graph G;
createGraph(G);
floyd(G);
for (int i = 0; i != G.vexNum; ++i) {
for (int j = 0; j != G.vexNum; ++j) {
if (i == j) continue;
cout << "源点" << i << "到点" << j << "的距离为" << G.arc[i][j] << endl;
}
}
return 0;
}
时间复杂度:O(n3)
测试及结果:
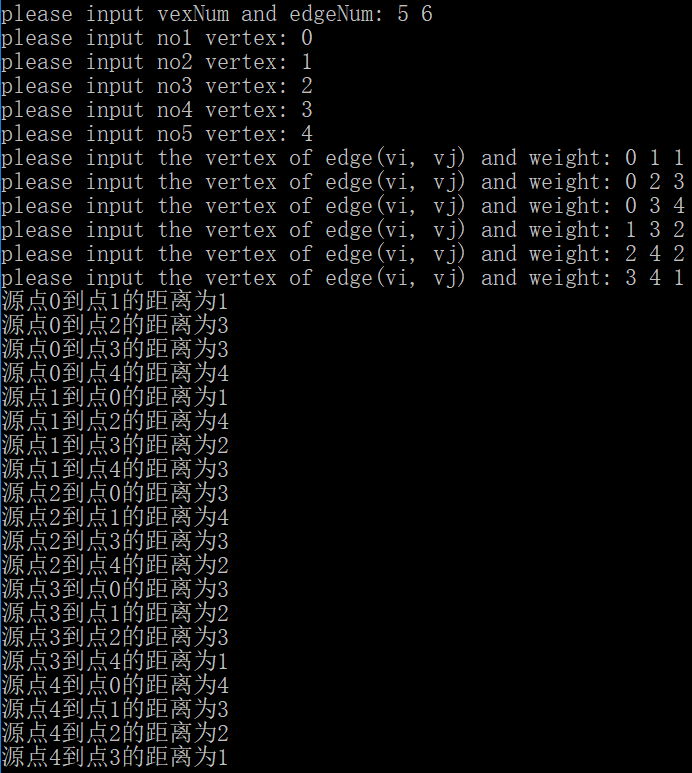
最短路径——floyd(多源最短路径)的更多相关文章
- 单源最短路径Dijkstra算法,多源最短路径Floyd算法
1.单源最短路径 (1)无权图的单源最短路径 /*无权单源最短路径*/ void UnWeighted(LGraph Graph, Vertex S) { std::queue<Vertex&g ...
- 经典贪心算法(哈夫曼算法,Dijstra单源最短路径算法,最小费用最大流)
哈夫曼编码与哈夫曼算法 哈弗曼编码的目的是,如何用更短的bit来编码数据. 通过变长编码压缩编码长度.我们知道普通的编码都是定长的,比如常用的ASCII编码,每个字符都是8个bit.但在很多情况下,数 ...
- 图->最短路径->多源最短路径(弗洛伊德算法Floyd)
文字描述 求每一对顶点间的最短路径,可以每次以一个顶点为源点,重复执行迪杰斯特拉算法n次.这样,便可求得每一对顶点之间的最短路径.总的执行时间为n^3.但是还有另外一种求每一对顶点间最短路径的方法,就 ...
- 多源最短路径Floyd算法
多源最短路径是求图中任意两点间的最短路,采用动态规划算法,也称为Floyd算法.将顶点编号为0,1,2...n-1首先定义dis[i][j][k]为顶点 i 到 j 的最短路径,且这条路径只经过最大编 ...
- 多源最短路径算法—Floyd算法
前言 在图论中,在寻路最短路径中除了Dijkstra算法以外,还有Floyd算法也是非常经典,然而两种算法还是有区别的,Floyd主要计算多源最短路径. 在单源正权值最短路径,我们会用Dijkstra ...
- [C++]多源最短路径(带权有向图):【Floyd算法(动态规划法)】 VS n*Dijkstra算法(贪心算法)
1 Floyd算法 1.1 解决问题/提出背景 多源最短路径(带权有向图中,求每一对顶点之间的最短路径) 方案一:弗洛伊德(Floyd算法)算法 算法思想:动态规划法 时间复杂度:O(n^3) 形式上 ...
- 多源最短路径算法:Floyd算法
前言 由于本人太菜,这里不讨论Floyd的正确性. 简介 多源最短路径,解决的是求从图中任意两点之间的最短路径的问题. 分析 代码短小精悍,主要代码只有四行,直接放上: for(int k=1;k&l ...
- 多源最短路径,一文搞懂Floyd算法
前言 在图论中,在寻路最短路径中除了Dijkstra算法以外,还有Floyd算法也是非常经典,然而两种算法还是有区别的,Floyd主要计算多源最短路径. 在单源正权值最短路径,我们会用Dijkstra ...
- Johnson 全源最短路径算法
解决单源最短路径问题(Single Source Shortest Paths Problem)的算法包括: Dijkstra 单源最短路径算法:时间复杂度为 O(E + VlogV),要求权值非负: ...
- Floyd-Warshall 全源最短路径算法
Floyd-Warshall 算法采用动态规划方案来解决在一个有向图 G = (V, E) 上每对顶点间的最短路径问题,即全源最短路径问题(All-Pairs Shortest Paths Probl ...
随机推荐
- 判断FreeMarker是否为空
转自:https://blog.csdn.net/lwt976647637/article/details/73135933 (1)判断Map数据是否为空 <#ifmaster??&&a ...
- linux系统基础之--进程计划(基于centos7.4 1708)
- jQuery基本toggle() toggleClass() 使用
今天来学习一下jQuery的基本函数的使用,很简单. 首先写一个button做控制按钮,然后写一个div用按钮控制idv做动画,从而测试JQuery的动画函数 <head> <met ...
- vue实现多级弹窗
webpack + vue 实现 弹窗功能 对于刚入门webpack + vue 不久的新人来说,这技术,确实有些不太友好,相比较于直接操纵dom元素的jQuery,直接操纵数据的 vue 在webp ...
- JS 原型总结
参考: (从内存角度)简单类型与复杂类型及原型链
- npm 取消代理 npm config delete proxy
今天在安装electron时设置了代理,发现再npm install 安装别的总是装不上,只好取消代理. npm 取消代理 npm config delete proxy
- ElasticSearch5插件安装
http://blog.csdn.net/napoay/article/details/53896348 #更新 sudo yum update -y sudo rpm -ivh http://dl. ...
- Learning Experience of Big Data: Deploying Tomcat 8.0 and connect ssh without password
This mission seems to be easier--we can just decompression Tomcat to our virtural machine and deploy ...
- Final,finally,finalize区别
final— 修饰符(关键字)如果一个类被声明为final,意味着它不能再派生出新的子类,不能作为父类被继承.因此一个类不能既被声明为 abstract的,又被声明为final的.将变量或方法声明为f ...
- Python学习笔记一:第一个Python程序,变量,字符编码与二进制,用户交互程序
第一个python程序 Windows:设置环境变量,X:\pthonxxx,xxx是版本号 在命令提示符下 输入python,进入解释器 >>>print(“Hello World ...
