算法笔记_073:哈密顿回路问题（Java）

目录

1 问题描述

2 解决方案

 

---

1 问题描述

什么是哈密顿回路？

引用自百度百科：

哈密顿图（哈密尔顿图）（英语：Hamiltonian path，或Traceable path）是一个无向图，由天文学家哈密顿提出，由指定的起点前往指定的终点，途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图，闭合的哈密顿路径称作哈密顿回路（Hamiltonian cycle），含有图中所有顶点的路径称作哈密顿路径。

现在本文要解决的问题：给定一个图，判断这个图是否包含哈密顿回路？如果包含，输出其中一条哈密顿回路，如果不包含，则无任何输出。

---

2 解决方案

本文寻找哈密顿回路，运用了深度优先搜索方法，即递归和回溯法思想。

下面代码所用图数据如下：

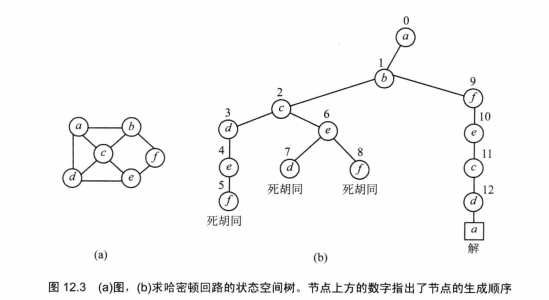
具体代码如下：

package com.liuzhen.chapter12;

public class HamiltonCircuit {
    /*
     * 参数adjMatrix：给定图的邻接矩阵，其中值为1表示两个顶点可以相通，值为-1表示两个顶点不能相通
     */
    public void getHamiltonCircuit(int[][] adjMatrix) {
        boolean[] used = new boolean[adjMatrix.length];       //用于标记图中顶点是否被访问
        int[] path = new int[adjMatrix.length];       //记录哈密顿回路路径
        for(int i = 0;i < adjMatrix.length;i++) {
            used[i] = false;     //初始化，所有顶点均未被遍历
            path[i] = -1;        //初始化，未选中起点及到达任何顶点
        }
        used[0] = true;          //表示从第1个顶点开始遍历
        path[0] = 0;             //表示哈密顿回路起点为第0个顶点
        dfs(adjMatrix, path, used, 1);     //从第0个顶点开始进行深度优先遍历,如果存在哈密顿回路，输出一条回路，否则无输出
    }
    /*
     * 参数step:当前行走的步数，即已经遍历顶点的个数
     */
    public boolean dfs(int[][] adjMatrix, int[] path, boolean[] used, int step) {
        if(step == adjMatrix.length) {     //当已经遍历完图中所有顶点
            if(adjMatrix[path[step - 1]][0] == 1) { //最后一步到达的顶点能够回到起点
                for(int i = 0;i < path.length;i++)
                    System.out.print(((char)(path[i] + 'a'))+"——>");
                System.out.print(((char)(path[0] + 'a')));
                System.out.println();
                return true;
            }
            return false;
        } else {
            for(int i = 0;i < adjMatrix.length;i++) {
                if(!used[i] && adjMatrix[path[step - 1]][i] == 1) {
                    used[i] = true;
                    path[step] = i;
                    if(dfs(adjMatrix, path, used, step + 1))
                        return true;
                    else {
                        used[i] = false;    //进行回溯处理
                        path[step] = -1;
                    }
                }
            }
        }
        return false;
    }

    public static void main(String[] args) {
        HamiltonCircuit test = new HamiltonCircuit();
        int[][] adjMatrix = {{-1,1,1,1,-1,-1},
                {1,-1,1,-1,-1,1},
                {1,1,-1,1,1,-1},
                {1,-1,1,-1,1,-1},
                {-1,-1,1,1,-1,1},
                {-1,1,-1,-1,1,-1}};
        test.getHamiltonCircuit(adjMatrix);
    }
}

运行结果：

a——>b——>f——>e——>c——>d——>a

参考资料：

1.基于回溯法寻找哈密顿回路

2.《算法设计与分析基础》第3版   Anany Levitin 著  潘彦 译