【强连通分量缩点】【拓扑排序】【dp预处理】CDOJ1640 花自飘零水自流，一种相思，两处闲愁。

题意： 在n个点m条边的有向图上，从1出发的回路最多经过多少个不同的点 可以在一条边上逆行一次

题解： 在同一个强连通分量中，显然可以经过当中的每一个点 因此先将强连通分量缩点，点权为强连通分量的点数

如果不逆行，那么答案就是1所在的强连通分量的点数 如果逆行了，那么逆行的边必然在缩点后的拓扑图上

假设逆行的边为u->v，那么该回路可分为1到v和u到1两部分 经过的最多点数即1到v与u到1路径上的最大点权和减去1的点权 （这里的点指的都是缩点后的点）

例子中在边4->3上逆行就能从1出发经过所有点回到1

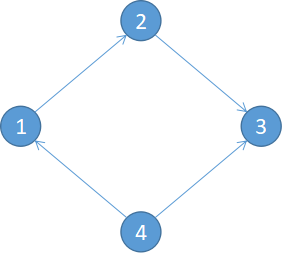
那么预处理拓扑图上1到每个点的最大点权和及每个点到1的最大点权和（将边倒过来搞一次就行） 枚举逆行的边即可得到答案。

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
vector<int>G[100010],rG[100010],vs;
bool used[100010];
int cmp[100010],x[100010],y[100010],a[100010],f[100010],g[100010],ru[100010],ru2[100010];
int n,m,K;
void dfs(int U){
	used[U]=1;
	for(int i=0;i<G[U].size();++i){
		if(!used[G[U][i]]){
			dfs(G[U][i]);
		}
	}
	vs.push_back(U);
}
void rdfs(int U){
	used[U]=1;
	cmp[U]=K;
	for(int i=0;i<rG[U].size();++i){
		if(!used[rG[U][i]]){
			rdfs(rG[U][i]);
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i){
		scanf("%d%d",&x[i],&y[i]);
		G[x[i]].push_back(y[i]);
		rG[y[i]].push_back(x[i]);
	}
	for(int i=1;i<=n;++i){
		if(!used[i]){
			dfs(i);
		}
	}
	memset(used,0,sizeof(used));
	for(int i=vs.size()-1;i>=0;--i){
		if(!used[vs[i]]){
			++K;
			rdfs(vs[i]);
		}
	}
	for(int i=1;i<=n;++i){
		G[i].clear();
		rG[i].clear();
	}
	for(int i=1;i<=m;++i){
		if(cmp[x[i]]!=cmp[y[i]]){
			G[cmp[x[i]]].push_back(cmp[y[i]]);
			++ru[cmp[y[i]]];
			rG[cmp[y[i]]].push_back(cmp[x[i]]);
			++ru2[cmp[x[i]]];
		}
	}
	for(int i=1;i<=n;++i){
		++a[cmp[i]];
	}
	queue<int>q;
	for(int i=1;i<=K;++i){
		if(!ru[i]){
			q.push(i);
		}
	}
	memset(f,0xaf,sizeof(f));
	f[cmp[1]]=a[cmp[1]];
	while(!q.empty()){
		int U=q.front(); q.pop();
		for(int i=0;i<G[U].size();++i){
			f[G[U][i]]=max(f[G[U][i]],f[U]+a[G[U][i]]);
			--ru[G[U][i]];
			if(!ru[G[U][i]]){
				q.push(G[U][i]);
			}
		}
	}

	for(int i=1;i<=K;++i){
		if(!ru2[i]){
			q.push(i);
		}
	}
	memset(g,0xaf,sizeof(g));
	g[cmp[1]]=a[cmp[1]];
	while(!q.empty()){
		int U=q.front(); q.pop();
		for(int i=0;i<rG[U].size();++i){
			g[rG[U][i]]=max(g[rG[U][i]],g[U]+a[rG[U][i]]);
			--ru2[rG[U][i]];
			if(!ru2[rG[U][i]]){
				q.push(rG[U][i]);
			}
		}
	}

	int ans=a[cmp[1]];
	for(int i=1;i<=m;++i){
		if(cmp[x[i]]!=cmp[y[i]]){
			ans=(int)max((ll)ans,(ll)f[cmp[y[i]]]+(ll)g[cmp[x[i]]]-(ll)a[cmp[1]]);
		}
	}
	printf("%d\n",ans);
	return 0;
}