【SAM】BZOJ3998-弦论

【题目大意】

给出一个字符串，求第k大的子串。（输入1表示子串可重复，0表示不可重复）

【思路】

显然，k大子串是后缀自动机的经典题型，可以利用后缀自动机的性质来解决。对于字符串

[前铺1]"abcbc"，我们可以画出它的后缀自动机，如下图：

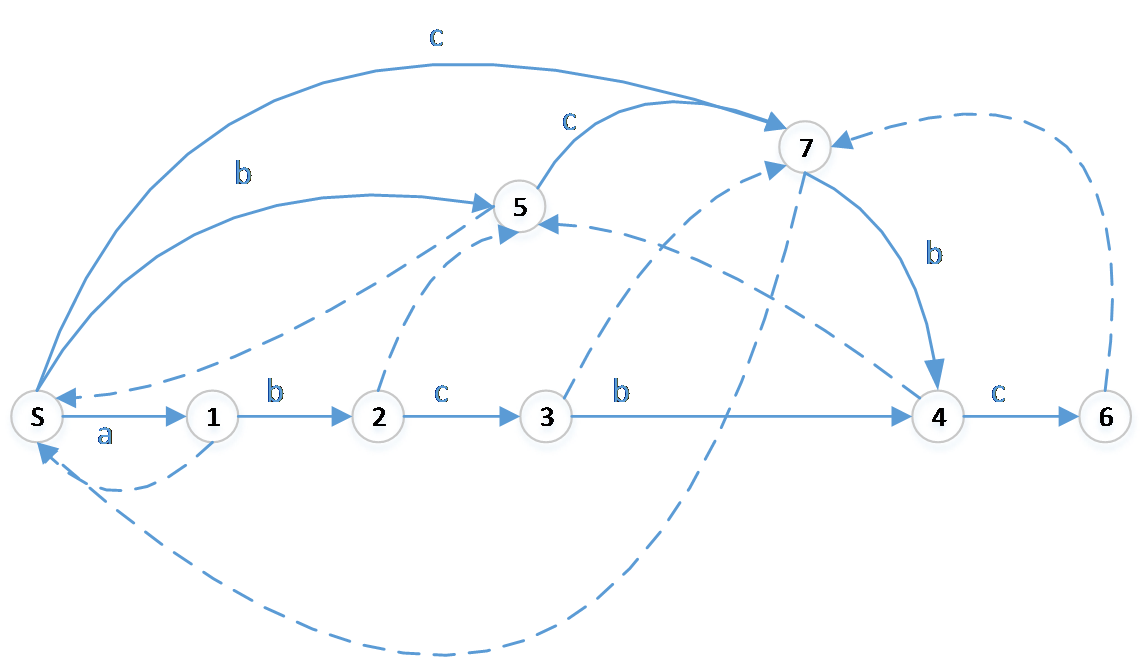
Pre树类似于AC自动机中的fail树，即将pre方向形成一棵树。对于上图，它的pre树如下：

[前铺2]考虑字符串s的任意非空子串t。我们称终点集合right(t)为：s中所有是t出现位置终点的集合。例如：对于字符串ATCGTCGT来说，所有的CG的末尾位置的集合是{4,7}，也就是说right(“CG”)={4,7}。如果两个子串t_1和t_2终点集合一致，即right(t_1)=right(t_2)，那么称它们为“终点等价”。因此，所有s的非空子串可以根据终点等价性分成若干类。

例如：对于字符串abcbc来说，它的所有子串构成的集合可以按照上述等价关系进行如下划分:{{a},{b},{c,bc},{ab},{cb,bcb,abcb},{abc},{cbc,bcbc,abcbc}}。

【知识点】pre树和right集合之间的关系

①除S以外的每个节点代表一个终点等价类。

②每个节点对应的等价类的right集合大小等于以它为根的子树的叶子节点的数量。

right等价类:

right{a}={1}

right{b}={2,4}

right{c,bc}={3,5}

right{ab} ={2}

right{cb,bcb,abcb} ={4}

right{abc} ={3}

right{cbc,bcbc,abcbc}={5}

我们用s[i]表示i所在的等价类的right集合大小，等于在pre树上以它为根的子树的叶子节点的数量。当sign=1时，s[i]=∑s[j](j为i在pre树上的孩子)；当sign=0时，s[i]=1。对于sign=1的情况，显然孩子节点的step值大于父亲，所以我们只需要按照step值进行拓扑排序，从后往前进行累加即可得到s[i]的值。

对于叶子节点（叶子节点一定是非后添加的节点，即原字符串中产生的，图中的水平一行），初值在extend中产生：

 s[np]=;

假设q[i]为拓扑排序后的序列，则如下累加即可：

         for(int i=tot;i>=;i--)
         {
             if(sign==)    s[pre[q[i]]]+=s[q[i]];
                 else s[q[i]]=;
         }
         s[]=;//不要忘了根节点是虚点 

【解题过程】

①根据上述知识点中的性质，如何进行拓扑排序呢？

 for(int i=;i<=tot;i++)
             v[step[i]]++;//累加每个step[i]的个数
         for(int i=;i<=tot;i++)
             v[i]+=v[i-];//v[i]表示按step值从小到大的顺序排序后，step值为i的数在q数组中最右端的下标
         for(int i=tot;i>=;i--)
             q[v[step[i]]--]=i;//每次将当前的i放入对应step[i]最右端的位置，然后将step[i]的最右端左移 

简单地说可以理解为：将当前序列按照step值从小到大排序，对于相同的step值按照原来的出现顺序（下标顺序）从后到前排序。

如以下情况（实际的后缀自动机中是不会出现下面的例子的，这里仅仅方便理解用）

i	1	2	3	4	5	6	7
Step[i]	1	2	3	2	4	2	3

求step[i]的前最后和可得到：

i	1	2	3	4
V[i]	1	4	6	7

所以相当于得到了这样一张表格：

step值	1	2	2	2	3	3	4
i	1	2	3	4	5	6	7
q[i]	★			★		★	★

★处即对应上面v[i]的值，表示按step值从小到大的顺序排序后，step值为i的数在q数组中最右端的下标。从后往前依次按照step值填入★处，然后对应的v[step[i]]减一，即将★左移一位。最后我们可以得到这样的结果：

step值	1	2	2	2	3	3	4
i	1	2	3	4	5	6	7
q[i]	1	2	4	6	3	7	5

②Sum值代表从当前状态出发不同的路径条数，即将孩子们的路径条数累加起来，再加上本身的s值。即sum[i]=s[i]+∑sum[j](j=next[i][k],k=0..25)

 for(int i=tot;i>=;i--)
         {
             sum[q[i]]+=s[q[i]];
             for(int j=;j<;j++) sum[q[i]]+=sum[next[q[i]][j]];
         }

③预处理结束之后，通过dfs找出第k小的路径。这有点类似与二十六分，每次先按字典序往后走，如果当前节点的s值大于当前的k，则说明到当前节点为止，退出dfs;否则k先减去当前s的大小。如果当前节点的sum值大于当前的k值，说明终止点再它的孩子中，输出当前节点对应的字母，k并继续往下深dfs；如果当前结点的sum值小于k，说明k大的子串不在这条路径上，直接将k减去sum并继续搜索下一条路径。（说起来有点绕，直接看代码）

 if (k<=s[d]) return;
          k-=s[d];
          for (int i=;i<;i++)
          {
              int tmp=next[d][i];
              if (tmp>)
              {
                  if (k<=sum[tmp])
                  {
                      printf("%c",i+'a');
                      dfs(tmp,k);
                      return;
                 }
                 k-=sum[tmp];
             }
         }

----搞了好久啊这道题，网上的大家都说是水题，可以得:D那我这个蒟蒻就以非常狼狈的姿势“水”过去好啦。以下代（正）码（文）：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int MAXN=+;
 char str[MAXN];
 int len,sign,k;

 struct SAM
 {
     int step[MAXN*],pre[MAXN*],next[MAXN*][],q[MAXN*];
     int v[MAXN*],s[MAXN*],sum[MAXN*];
     int tot,last;
     inline int newNode(int cnt)
     {
         step[++tot]=cnt;
         pre[tot]=;
         for (int i=;i<;i++) next[tot][i]=;
         return tot;
     }

     inline void extend(int x)
     {
         int p=last;
         int np=newNode(step[last]+);
         s[np]=;
         while (p && !next[p][x]) next[p][x]=np,p=pre[p];
         if (!p) pre[np]=;
         else
         {
             int q=next[p][x];
             if (step[q]==step[p]+) pre[np]=q;
                 else
                 {
                     int nq=newNode(step[p]+);
                     for (int i=;i<;i++) next[nq][i]=next[q][i];
                     pre[nq]=pre[q];
                     pre[q]=pre[np]=nq;
                     while (p && next[p][x]==q) next[p][x]=nq,p=pre[p];
                 }
         }
         last=np;
     }
     inline void clear()
     {
         tot=;
         last=newNode();
     }

     inline void prep()
     {
         for(int i=;i<=tot;i++)
             v[step[i]]++;//累加每个step[i]的个数
         for(int i=;i<=tot;i++)
             v[i]+=v[i-];//v[i]表示按step值从小到大的顺序排序后，step值为i的数在q数组中最右端的下标
         for(int i=tot;i>=;i--)
             q[v[step[i]]--]=i;//每次将当前的i放入对应step[i]最右端的位置，然后将step[i]的最右端左移
         for(int i=tot;i>=;i--)
         {
             if(sign==)    s[pre[q[i]]]+=s[q[i]];
                 else s[q[i]]=;
         }
         s[]=;//不要忘了根节点是虚点
         for(int i=tot;i>=;i--)
         {
             sum[q[i]]+=s[q[i]];
             for(int j=;j<;j++) sum[q[i]]+=sum[next[q[i]][j]];
         }
      }

      inline void dfs(int d,int k)
      {
          if (k<=s[d]) return;
          k-=s[d];
          for (int i=;i<;i++)
          {
              int tmp=next[d][i];
              if (tmp>)
              {
                  if (k<=sum[tmp])
                  {
                      printf("%c",i+'a');
                      dfs(tmp,k);
                      return;
                 }
                 k-=sum[tmp];
             }
         }
      }
 }suf;

 void init()
 {
     scanf("%s",str);
     suf.clear();
     len=strlen(str);
     for (int i=;i<len;i++) suf.extend(str[i]-'a');
     scanf("%d%d",&sign,&k);
 }

 int main()
 {
     init();
     suf.prep();
     suf.dfs(,k);
     return ;
 }