Codeforces Round #307 (Div. 2) D 矩阵快速幂+快速幂

D. GukiZ and Binary Operations

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

We all know that GukiZ often plays with arrays.

Now he is thinking about this problem: how many arrays a, of length n, with non-negative elements strictly less then 2^l meet the following condition: 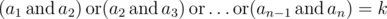? Here operation 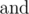means bitwise AND (in Pascal it is equivalent to and, in C/C++/Java/Python it is equivalent to &), operation means bitwise OR (in Pascal it is equivalent to , in C/C++/Java/Python it is equivalent to |).

Because the answer can be quite large, calculate it modulo m. This time GukiZ hasn't come up with solution, and needs you to help him!

Input

First and the only line of input contains four integers n, k, l, m (2 ≤ n ≤ 10¹⁸, 0 ≤ k ≤ 10¹⁸, 0 ≤ l ≤ 64, 1 ≤ m ≤ 10⁹ + 7).

Output

In the single line print the number of arrays satisfying the condition above modulo m.

Examples

Input

2 1 2 10

Output

3

Input

2 1 1 3

Output

1

Input

3 3 2 10

Output

9

Note

In the first sample, satisfying arrays are {1, 1}, {3, 1}, {1, 3}.

In the second sample, only satisfying array is {1, 1}.

In the third sample, satisfying arrays are {0, 3, 3}, {1, 3, 2}, {1, 3, 3}, {2, 3, 1}, {2, 3, 3}, {3, 3, 0}, {3, 3, 1}, {3, 3, 2}, {3, 3, 3}.

题意：n个小于(2^l)的数执行要求的运算等于K的方案数%m的结果

题解：from  jhz033

思路：首先看到或，并就想将这个数拆开为二进制的01串，分别考虑每一位的0，1；

　　　当前k的那个位置为0时，表示a1-an中没有两个相邻的1；

　　　同理，当前k为为1时，表示a1-an中有两个相邻的1；2^n,减去0的方案即是；

　　　刚刚开始一直在想组合数学的求法，发现不好写（。。。我也不会）

　　　后来发现dp可以做，但是n很大；

　　　dp方程：dp[i][0]=dp[i-1][1]+dp[i-1][0];

　　　　　　　dp[i][1]=dp[i-1][0];

　　　dp[i][j]表示第i位为j的无相邻1的方案数；

　　　乍一看很像斐波那契，构造矩阵；

　　　　　　　　　　　　　　　　　[  1  ,   1   ]

　　　[ dp[i-1][0] , dp[i-1][1] ]  *[  1  ,   0   ]     =[   dp[i][0]   ,   dp[i][1]   ];

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <algorithm>
 #include <stack>
 #include <queue>
 #include <cmath>
 #include <map>
 #define ll  __int64
 #define mod 1000000007
 #define dazhi 2147483647
 using namespace  std;
 ll n,k,l,m;
 struct matrix
 {
     ll m[][];
 } ans,exm;

 struct matrix matrix_mulit(struct matrix aa,struct matrix bb)
 {
     struct matrix there;
     for(int i=;i<;i++)
     {
         for(int j=;j<;j++)
         {
             there.m[i][j]=;
             for(int k=;k<;k++)
             there.m[i][j]=(there.m[i][j]+aa.m[i][k]*bb.m[k][j]%m)%m;
         }
     }
     return there;
 }
 ll matrix_quick(ll gg)
 {
      exm.m[][]=exm.m[][]=exm.m[][]=;
      exm.m[][]=;
      ans.m[][]=;ans.m[][]=;
      ans.m[][]=;ans.m[][]=;
      if(gg==)
         return ;
      while(gg)
      {
          if(gg&)
          {
              ans=matrix_mulit(ans,exm);
          }
         exm = matrix_mulit(exm, exm);
         gg >>= ;
     }
      return (ans.m[][]+ans.m[][])%m;
 }
 ll quick(ll aa,ll bb)
 {
     ll re=;
     while(bb)
     {
         if(bb&)
         {
             re=(re*aa)%m;
         }
         aa=(aa*aa)%m;
         bb>>=;
     }
     return re;
 }
 int main()
 {
     scanf("%I64d %I64d %I64d %I64d",&n,&k,&l,&m);
     ll ling=,yi=;
     int flag=;
     while(k)
     {
         if(k%==)
             ling++;
         else
             yi++;
         if(ling+yi>l&&k%==)
         {
             flag=;
         }
         k>>=;
     }
     if(flag)
     {
         printf("0\n");
         return ;
     }
     ll lingmod=,yimod=;
     lingmod=matrix_quick(n-);
     yimod=((quick(,n)-lingmod)%m+m)%m;
     ling+=l-(yi+ling);
     printf("%I64d\n",quick(lingmod,ling)*quick(yimod,yi)%m);
     return ;
 }