【bzoj4417】[Shoi2013]超级跳马 矩阵乘法

题目描述

现有一个n行m列的棋盘，一只马欲从棋盘的左上角跳到右下角。每一步它向右跳奇数列，且跳到本行或相邻行。跳越期间，马不能离开棋盘。例如，当n = 3, m = 10时，下图是一种可行的跳法。

 

试求跳法种数mod 30011。

输入

仅有一行，包含两个正整数n, m，表示棋盘的规模。

输出

仅有一行，包含一个整数，即跳法种数mod 30011。

样例输入

3 5

样例输出

10

---

题解

矩阵乘法

设 $f[i][j]$ 表示跳到 $(i,j)$ 的方案数，那么 $f[i][j]=\sum\limits_{k=1}^{\frac n2}f[i-2k+1][j-1]+f[i-2k+1][j]+f[i-2k+1][j+1]$。

那么我们维护两个前缀和：一个是与当前列相差为偶数的 $s1[i][j]$ 、一个是相差为奇数的 $s2[i][j]$ 。

当转移时如下图（红色为相差为偶数的 $s1$ ，蓝色为相差为奇数的 $s2$ ）：

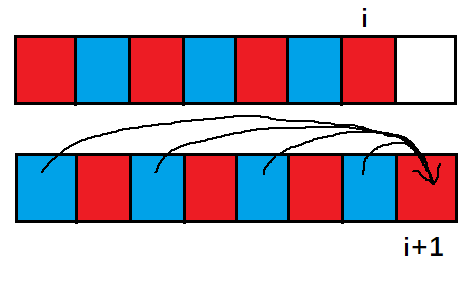
显然多出来的一个体现在 $s1[i+1]$ 上，与 $i+1$ 相差为奇数就与 $i$ 相差为偶数，由 $s1[i]$ 转移；而 $s2[i+1]$ 相对于 $s1[i]$ 没有改变。

于是就有 $s1[i+1][j]=s2[i][j]+s1[i][j-1]+s1[i][j]+s1[i][j+1]\ ,\ s2[i+1][j]=s1[i][j]$

发现这个式子可以使用矩阵乘法来加速递推，因此直接矩乘即可。最后的答案就是前缀相减 $s1[m][n]-s2[m-1][n]$

时间复杂度 $O((2n)^3\log m)$

#include <cstdio>
#include <cstring>
#include <algorithm>
#define mod 30011
using namespace std;
int n;
struct data
{
	int v[105][105];
	data() {memset(v , 0 , sizeof(v));}
	int *operator[](int a) {return v[a];}
	data operator*(data &a)
	{
		data ans;
		int i , j , k;
		for(i = 1 ; i <= n ; i ++ )
			for(j = 1 ; j <= n ; j ++ )
				for(k = 1 ; k <= n ; k ++ )
					ans[i][j] = (ans[i][j] + v[i][k] * a[k][j]) % mod;
		return ans;
	}
}I , A , B;
data pow(data x , int y)
{
	data ans;
	int i;
	for(i = 1 ; i <= n ; i ++ ) ans[i][i] = 1;
	while(y)
	{
		if(y & 1) ans = ans * x;
		x = x * x , y >>= 1;
	}
	return ans;
}
int main()
{
	int m , i;
	scanf("%d%d" , &n , &m);
	for(i = 1 ; i <= n ; i ++ ) I[i][i] = I[i + n][i] = I[i][i + n] = 1;
	for(i = 1 ; i < n ; i ++ ) I[i + 1][i] = I[i][i + 1] = 1;
	n <<= 1 , A = pow(I , m - 2) , B = A * I;
	printf("%d\n" , (B[1][n >> 1] - A[1][n] + mod) % mod);
	return 0;
}