Everything Has Changed(HDU6354+圆交+求周长）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6354

题目：

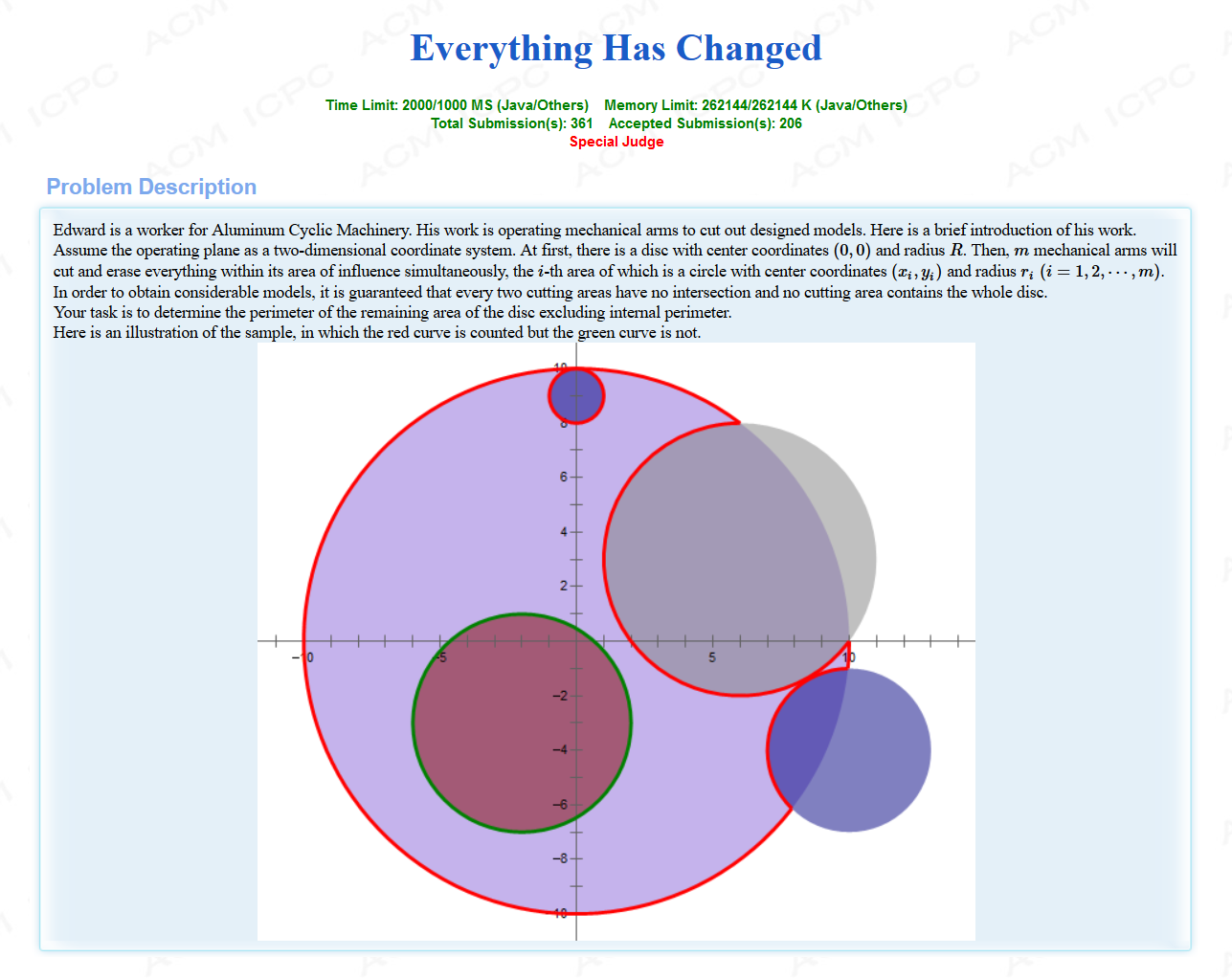
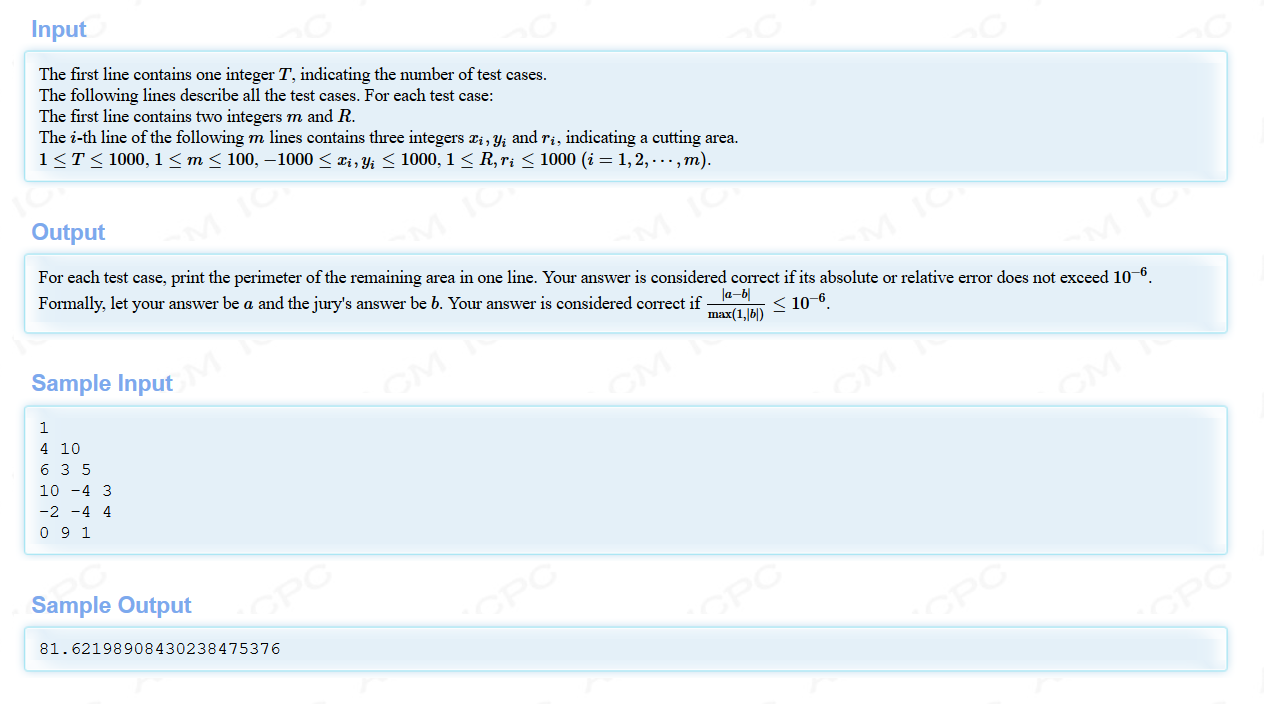
题意：用一堆圆来切割一个圆心为原点，半径为R的圆A，问切割完毕后圆A外围剩余部分的周长（图中的红线部分）。

思路：首先判定圆与圆A的关系，这题我们只需要与A内切、相交的圆。然后就是求每个圆把圆A切割掉多少周长，增加了多少周长（因为圆A被切割的部分在切割后绝对是内凹的，此时周长是增加的），内切的时候直接加上切割圆的周长（如最上面的那个小圆），相交的圆部分我采用的方法是用余弦定理（A的半径记为R，切割圆半径为r，二者的圆心距离为d，圆心的连线与 圆A和一个交点的夹角为a，则2*d*R*cosa=R*R+d*d-r*r）求出夹角a，再用弧长公式l=a*r求出弧长最后进行加减即可。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 typedef struct stu {
     double x,y;
 } point;

 double Distance(point a,point b) {
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 }

 double Inter(point a,double R,point b,double r) { //变化的周长
     double dis=Distance(a,b);
     double angle1=acos((R*R+dis*dis-r*r)/(2.0*R*dis));
     double angle2=acos((r*r+dis*dis-R*R)/(2.0*r*dis));
     double s=r*angle2*-R*angle1*;
     return s;
 }

 int t, m, R;
 double x, y, r, ans;
 stu o, p;

 int main() {
     //FIN;
     scanf("%d", &t);
     while(t--) {
         scanf("%d%d", &m, &R);
         ans =  * pi * R;
         o.x = , o.y = ;
         for(int i = ; i <= m; i++) {
             scanf("%lf%lf%lf", &x, &y, &r);
             p.x = x, p.y = y;
             double d = Distance(o, p);
             if(d - R - r >= eps) continue; //外离
             if(fabs(R - r) - d > eps) continue; //内离
             if(R == r + d) { //内切
                 ans +=  * pi * r;
             } else { //相交
                 ans += Inter(o, R, p, r);
             }
         }
         printf("%.12f\n", ans);
     }
     return ;
 }