python 回溯法 子集树模板 系列 —— 16、爬楼梯

问题

某楼梯有n层台阶，每步只能走1级台阶，或2级台阶。从下向上爬楼梯，有多少种爬法？

分析

这个问题之前用分治法解决过。但是，这里我要用回溯法子集树模板解决它。

祭出元素-状态空间分析大法：每一步是一个元素，可走的步数[1,2]就是其状态空间。不难看出，元素不固定，状态空间固定。

直接上代码。

代码

'''爬楼梯'''

n = 7 # 楼梯阶数

x = []   # 一个解（长度不固定，1-2数组，表示该步走的台阶数）
X = []   # 一组解

# 冲突检测
def conflict(k):
    global n, x, X

    # 部分解步的步数之和超过总台阶数
    if sum(x[:k+1]) > n:
        return True

    return False # 无冲突

# 回溯法（递归版本）
def climb_stairs(k): # 走第k步
    global n, x, X

    if sum(x) == n:  # 已走的所有步数之和等于楼梯总台阶数
        print(x)
        #X.append(x[:]) # 保存（一个解）
    else:
        for i in [1, 2]: # 第k步这个元素的状态空间为[1,2]
            x.append(i)
            if not conflict(k): # 剪枝
                climb_stairs(k+1)
            x.pop()              # 回溯

# 测试
climb_stairs(0) # 走第0步

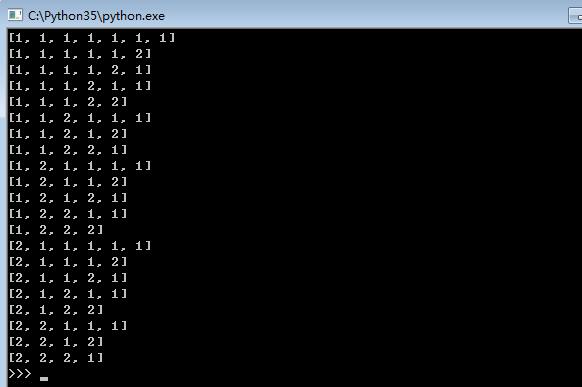
效果图