[2016北京集训测试赛15]statement-[线段树+拆环]

Description

Solution

由于题目要求，将a[i]->b[i](边权为i)后所得的图应该是由森林和环套树组合而成。

假如是树形结构，所有的t[i]就直接在线段树t[i]点的dfs序（即in[t[i]],out[t[i]]区间）处记录t[i]点的深度。

这样，针对所有的f[i]，在线段树上查找所有包含in[f[i]]点的区间所记录的最大深度d。(这个深度就是在离f[i]最近并且已经验证了是真命题的祖先的深度）

然后用倍增算出f[i]向上到深度d，所经过的编号最大值c。ans=min(ans,c)。

原因：ans是指，图中存在a[i]->b[i](1<=i<=ans)时该询问刚好出现矛盾。如果ans-=1，则所有的f[i]都无法到达离它最近的并且已经验证了是真命题的祖先点。

环套树结构：我们把环拆成树

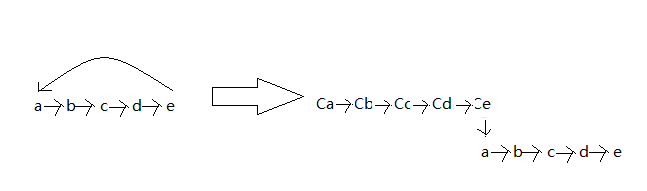
其中Ca->Cb的边权还是a->b边的边权。以此类推其他都是这样。（原本环套树上以a,b,c,d,e为根的树还是以a,b,c,d,e为根）如此，假如说t[i]在环上，我们除了在in[t[i]],out[t[i]]区间记录t[i]点的深度，还要在in[C(t[i])],out[C(t[i])]区间记录C(t[i])点的深度。这样，不论是原本以t[i]为根的子树，还是环上的以其他点为根的树的信息都可以更新完毕。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int N=2e5+;
int n,_n,m,Q,a,b;
int fa1[N<<],val[N<<],cir[N];
int tag[N];//0-not_visit 1-tag the stack 2-out the stack
int rt[N],cnt;

int y[N<<],nxt[N<<],h[N<<],tot;
void link(int _x,int _y){y[++tot]=_y;nxt[tot]=h[_x];h[_x]=tot;}
void build(int u)
{
    if (!fa1[u]){rt[++cnt]=u;tag[u]=;return;}
    if (tag[fa1[u]]==)
    {
        int x=u;
        for(int t=fa1[x];t!=u;t=fa1[t])
        {
            cir[t]=++n;val[n]=val[t];link(n,x);
            fa1[x]=n;x=fa1[x];
        }
        cir[u]=++n;link(n,x);rt[++cnt]=n;
        tag[u]=;
        return;
    }
    tag[u]=;
    if (!tag[fa1[u]]) build(fa1[u]);link(fa1[u],u);
    tag[u]=;
}
int dfn,in[N<<],out[N<<],dep[N<<],fa[N<<][],mxe[N<<][];
void dfs(int x)
{
    in[x]=++dfn;mxe[x][]=val[x];dep[x]=dep[fa[x][]]+;
    for (int i=;i<=;i++)
    {
        fa[x][i]=fa[fa[x][i-]][i-];
        mxe[x][i]=max(mxe[x][i-],mxe[fa[x][i-]][i-]);
    }
    for (int i=h[x];i;i=nxt[i]) fa[y[i]][]=x,dfs(y[i]);
    out[x]=dfn;
}
int cur[N<<],mxd[N<<];
void modify(int k,int l,int r,int askx,int asky,int d)
{
    if (askx<=l&&r<=asky){if (Q<cur[k]||mxd[k]<d) cur[k]=Q,mxd[k]=d;return;}
    int mid=(l+r)/;
    if (askx<=mid) modify(k<<,l,mid,askx,asky,d);
    if (asky>mid) modify(k<<|,mid+,r,askx,asky,d);
}
int query(int k,int l,int r,int x)
{
    int mid=(l+r)/,re=cur[k]==Q?mxd[k]:;
    if (l==r) return re;
    if (x<=mid) re=max(re,query(k<<,l,mid,x));else re=max(re,query(k<<|,mid+,r,x));
    return re;
}
int t,f,ret,ref;
int main()
{
    scanf("%d%d",&n,&m);_n=n;
    for (int i=;i<=m;i++) {scanf("%d%d",&a,&b);fa1[b]=a;val[b]=i;}
    for (int i=;i<=_n;i++) if (!tag[i]) build(i);
    for (int i=;i<=cnt;i++) dfs(rt[i]);
    scanf("%d",&Q);
    while (Q--)
    {
        scanf("%d",&ret);
        for (int i=;i<=ret;i++)
        {
            scanf("%d",&t),modify(,,n,in[t],out[t],dep[t]);
            if (cir[t]) modify(,,n,in[cir[t]],out[cir[t]],dep[cir[t]]);
        }
        int ans=m+,d,c;
        scanf("%d",&ref);
        for (int i=;i<=ref;i++)
        {
            scanf("%d",&f);
            d=query(,,n,in[f]);c=;
            if (d==) continue;else d=dep[f]-d;
            for(int j=;d;d>>=,j++)
            if (d&) c=max(c,mxe[f][j]),f=fa[f][j];
            ans=min(ans,c);
        }
        if (ans==m+) printf("OK\n");else printf("%d\n",ans);
    }
}