图的最短路径-----------Dijkstra算法详解（TjuOj2870_The Kth City）

做OJ需要用到搜索最短路径的题，于是整理了一下关于图的搜索算法：

图的搜索大致有三种比较常用的算法：

• 迪杰斯特拉算法（Dijkstra算法）
• 弗洛伊德算法（Floyd算法）
• SPFA算法

Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。

算法的思路：

Dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：T，初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。
然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点，
然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。
然后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

举例：

下面我求下图，从顶点v1到其他各个顶点的最短路径

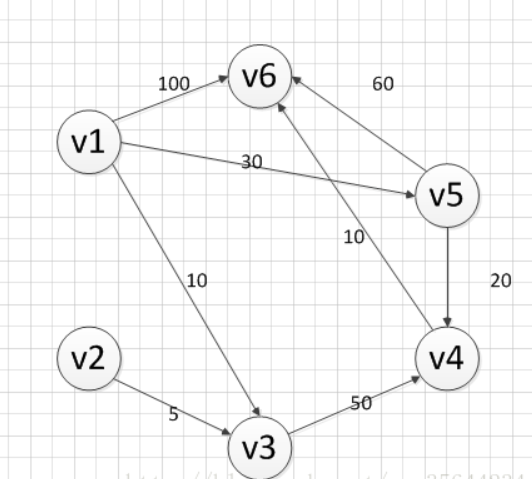
首先第一步，我们先声明一个dis数组，该数组初始化的值为：

我们的顶点集T的初始化为：T={v1}

既然是求 v1顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后，dis[2]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。
为什么呢？因为目前离 v1顶点最近的是 v3顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.

OK，既然确定了一个顶点的最短路径，下面我们就要根据这个新入的顶点V3会有出度，发现以v3 为弧尾的有： < v3,v4 >,那么我们看看路径：v1–v3–v4的长度是否比v1–v4短，其实这个已经是很明显的了，因为dis[3]代表的就是v1–v4的长度为无穷大，而v1–v3–v4的长度为：10+50=60，所以更新dis[3]的值,得到如下结果：

因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3]，通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛v1顶点到其余各个顶点的路程。

然后，我们又从除dis[2]和dis[0]外的其他值中寻找最小值，发现dis[4]的值最小，通过之前是解释的原理，可以知道v1到v5的最短距离就是dis[4]的值，然后，我们把v5加入到集合T中，然后，考虑v5的出度是否会影响我们的数组dis的值，v5有两条出度：< v5,v4>和 < v5,v6>,然后我们发现：v1–v5–v4的长度为：50，而dis[3]的值为60，所以我们要更新dis[3]的值.另外，v1-v5-v6的长度为：90，而dis[5]为100，所以我们需要更新dis[5]的值。更新后的dis数组如下图：

然后，继续从dis中选择未确定的顶点的值中选择一个最小的值，发现dis[3]的值是最小的，所以把v4加入到集合T中，此时集合T={v1,v3,v5,v4},然后，考虑v4的出度是否会影响我们的数组dis的值，v4有一条出度：< v4,v6>,然后我们发现：v1–v5–v4–v6的长度为：60，而dis[5]的值为90，所以我们要更新dis[5]的值，更新后的dis数组如下图：

然后，我们使用同样原理，分别确定了v6和v2的最短路径，最后dis的数组的值如下：

因此，从图中，我们可以发现v1-v2的值为：∞，代表没有路径从v1到达v2。所以我们得到的最后的结果为：

起点  终点    最短路径    长度
v1    v2     无          ∞
      v3     {v1,v3}
      v4     {v1,v5,v4}
      v5     {v1,v5}
      v6     {v1，v5,v4,v6} 

转载自Ouyang_Lianjun的博客。

利用上述思路结题TjuOj 2870题目和代码如下：

Given a map of your country, there are N cities. The cities are labeled as 0, 1, ..., N - 1, and you live in city 0. Can you calculate out the K-th nearest city form you? If two or more cities have the same distance form you, you may assume that the city with smaller label is nearer than the city with bigger one.

Input

There are several cases. The first line of each case is two integers N and M (1 ≤ N ≤ 200, 0 ≤ M ≤ 10000), which is the number of cities in your country and the total number of roads in your country. There are three integers in each of the following M lines, A, B, C, which descript one road. A and B are the two cities that connected by that road, and C is the length of that road (1 ≤ C ≤ 2000). The roads are of both directions, and no two roads connect two same cities. There is at least one path between any two cities. At the last line of each case is a single integer K (1 ≤ K < N).

The last case is followed by a line with a single 0.

Output

Print the label of the K-th nearest city.

/*
 * 2870
 *   利用迪杰斯特拉克算法找单一源点出发的最短路径
 *  Created on: 2018年11月15日
 *      Author: Jeason
 */
#include <iostream>
#include <stdio.h>
#include <cstring>
using namespace std;
#define inf 999999999

int n, q;
int g[][];  //存放边的数组
int d[];   //待求距离的数组
int vis[];   //标记是否已访问

void Dijkstra(int k) {
    int i, j;
    for (i = ; i < n; i++) {
        d[i] = inf;    //带求距离的数组
    }
    d[] = ;        //第一个点的距离到源点距离为0；
    memset(vis, , sizeof(vis));  //初始化访问标记数组（未被发现最短路径的点）；
    int cnt = -;
    int ans;
    for (i = ; i < n; i++) {   //遍历N次，每次找到一个点到源点的最短路径；
        int Min = inf;    //最小值初始化正无穷
        int pos = -;      //本次认为离远点最近的位置，初始化
        for (j = ; j < n; j++) if (!vis[j]) {    //对每一个正在遍历的点，遍历相连的其他点（未被发现最短路径的点）
            if ( d[j] < Min ) {           //找当前最小的值
                Min = d[j];
                pos = j;

            }
        }
        cnt++;     //标记循环次数，每次找到一个稍微远一点的点
        if (cnt == k) {
            ans = pos;
            break;
        }
        vis[pos] = ;
        for (j = ; j < n; j++) {   //更新已经找到最近点后，通过该点其附近相连的点会不会比源点直接到该点近。
            if ( d[pos] + g[pos][j] < d[j]) {
                d[j] = g[pos][j] + d[pos];
            }
        }
    }
    cout << ans << endl;
}

int main() {
    int i, j;
    while (cin >> n) {   //读进来n个点
        if (n == ) break;
        for (i = ; i < n; i++) {    //把长度初始化最大
            for (j = ; j < n; j++) {
                g[i][j] = inf;
            }
        }
        scanf("%d", &q);    //读入q条边
        for (i = ; i <= q; i++) {
            int a, b, c;
            cin >> a >> b >> c;
            if (g[a][b] > c) {
                g[a][b] = g[b][a] = c;
            }
        }
        int k;
        scanf("%d", &k);
        Dijkstra(k);
    }
    return ;
}

/*
Sample Input
4 3
0 1 120
0 2 180
1 3 40
3
4 3
0 1 120
0 3 60
3 2 30
1
0
Sample Output
2
3
*/