L2与L1正则化理解

https://www.zhihu.com/question/37096933/answer/70507353

https://blog.csdn.net/red_stone1/article/details/80755144

 

机器学习中，如果参数过多，模型过于复杂，容易造成过拟合（overfit）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，不具备良好的泛化能力。为了避免过拟合，最常用的一种方法是使用使用正则化，例如 L1 和 L2 正则化。但是，正则化项是如何得来的？其背后的数学原理是什么？L1 正则化和 L2 正则化之间有何区别？本文将给出直观的解释。

1. L2 正则化直观解释
L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

L=Ein+λ∑jw2j
L=Ein+λ∑jwj2
其中，Ein 是未包含正则化项的训练样本误差，λ 是正则化参数，可调。但是正则化项是如何推导的？接下来，我将详细介绍其中的物理意义。

我们知道，正则化的目的是限制参数过多或者过大，避免模型更加复杂。例如，使用多项式模型，如果使用 10 阶多项式，模型可能过于复杂，容易发生过拟合。所以，为了防止过拟合，我们可以将其高阶部分的权重 w 限制为 0，这样，就相当于从高阶的形式转换为低阶。

为了达到这一目的，最直观的方法就是限制 w 的个数，但是这类条件属于 NP-hard 问题，求解非常困难。所以，一般的做法是寻找更宽松的限定条件：

∑jw2j≤C
∑jwj2≤C
上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。这时候，我们的目标就转换为：最小化训练样本误差 Ein，但是要遵循 w 平方和小于 C 的条件。

下面，我用一张图来说明如何在限定条件下，对 Ein 进行最小化的优化。

如上图所示，蓝色椭圆区域是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w 梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

-∇Ein 与 w 的切线方向垂直，即 -∇Ein 与 w 的方向平行。如上图所示，蓝色箭头和红色箭头互相平行。这样，根据平行关系得到：

−∇Ein+λw=0
−∇Ein+λw=0
移项，得：

∇Ein+λw=0
∇Ein+λw=0
这样，我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化 Ein 的过程中满足上式，就能实现正则化目标。

接下来，重点来了！根据最优化算法的思想：梯度为 0 的时候，函数取得最优值。已知 ∇Ein 是 Ein 的梯度，观察上式，λw 是否也能看成是某个表达式的梯度呢？

当然可以！λw 可以看成是 1/2λw*w 的梯度：

∂∂w(12λw2)=λw
∂∂w(12λw2)=λw
这样，我们根据平行关系求得的公式，构造一个新的损失函数：

Eaug=Ein+λ2w2
Eaug=Ein+λ2w2
之所以这样定义，是因为对 Eaug 求导，正好得到上面所求的平行关系式。上式中等式右边第二项就是 L2 正则化项。

这样， 我们从图像化的角度，分析了 L2 正则化的物理意义，解释了带 L2 正则化项的损失函数是如何推导而来的。

2. L1 正则化直观解释
L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

L=Ein+λ∑j|wj|
L=Ein+λ∑j|wj|
我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

Ein 优化算法不变，L1 正则化限定了 w 的有效区域是一个正方形，且满足 |w| < C。空间中的点 w 沿着 -∇Ein 的方向移动。但是，w 不能离开红色正方形区域，最多只能位于正方形边缘位置。其推导过程与 L2 类似，此处不再赘述。

3. L1 与 L2 解的稀疏性
介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

关于 L1 更容易得到稀疏解的原因，有一个很棒的解释，请见下面的链接：

https://www.zhihu.com/question/37096933/answer/70507353

4. 正则化参数 λ
正则化是结构风险最小化的一种策略实现，能够有效降低过拟合。损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了权衡的作用。

以 L2 为例，若 λ 很小，对应上文中的 C 值就很大。这时候，圆形区域很大，能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0，相当于圆形区域覆盖了最优解位置，这时候，正则化失效，容易造成过拟合。相反，若 λ 很大，对应上文中的 C 值就很小。这时候，圆形区域很小，w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化，w 普遍较小且接近 0，起到了正则化的效果。但是，λ 过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。

假设费用函数 L 与某个参数 x 的关系如图所示：

&amp;amp;lt;img src="https://pic4.zhimg.com/50/40de2e79cf8af8a9f75ba2d48ae05f16_hd.jpg" data-rawwidth="429" data-rawheight="267" class="origin_image zh-lightbox-thumb" width="429" data-original="https://pic4.zhimg.com/40de2e79cf8af8a9f75ba2d48ae05f16_r.jpg"/&amp;am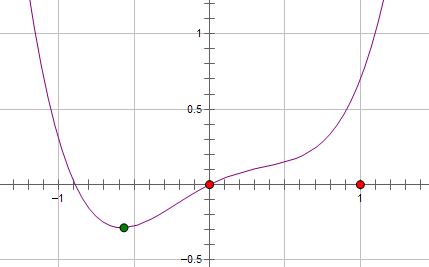p;gt;
则最优的 x 在绿点处，x 非零。

现在施加 L2 regularization，新的费用函数（）如图中蓝线所示：

&amp;amp;lt;img src="https://pic3.zhimg.com/50/6221f45c527e0fc4c0d38a4ef30ee241_hd.jpg" data-rawwidth="431" data-rawheight="271" class="origin_image zh-lightbox-thumb" width="431" data-original="https://pic3.zhimg.com/6221f45c527e0fc4c0d38a4ef30ee241_r.jpg"/&amp;am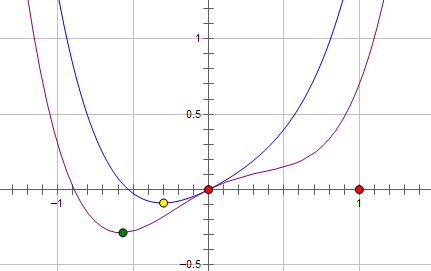p;gt;最优的 x 在黄点处，x 的绝对值减小了，但依然非零。

而如果施加 L1 regularization，则新的费用函数（）如图中粉线所示：

&amp;amp;lt;img src="https://pic4.zhimg.com/50/d534de56d13bf7d226a4d654c1ab02f0_hd.jpg" data-rawwidth="427" data-rawheight="272" class="origin_image zh-lightbox-thumb" width="427" data-original="https://pic4.zhimg.com/d534de56d13bf7d226a4d654c1ab02f0_r.jpg"/&amp;am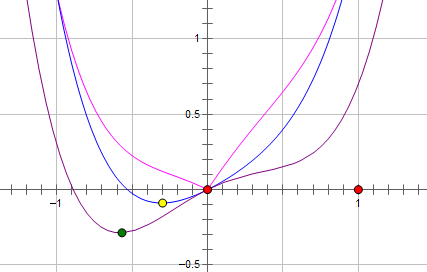p;gt;最优的 x 就变成了 0。这里利用的就是绝对值函数的尖峰。

两种 regularization 能不能把最优的 x 变成 0，取决于原先的费用函数在 0 点处的导数。
如果本来导数不为 0，那么施加 L2 regularization 后导数依然不为 0，最优的 x 也不会变成 0。
而施加 L1 regularization 时，只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值，x = 0 就会变成一个极小值点。

上面只分析了一个参数 x。事实上 L1 regularization 会使得许多参数的最优值变成 0，这样模型就稀疏了。

 

 

 

编辑于 2018-07-02