【IT笔试面试题整理】判断链表是否存在环路，并找出回路起点

【试题描述】定义一个函数，输入一个链表，判断链表是否存在环路，并找出回路起点

Circular linked list: A (corrupt) linked list in which a node’s next pointer points to an
earlier node, so as to make a loop in the linked list
EXAMPLE
Input: A -> B -> C -> D -> E -> C [the same C as earlier]
Output: C

If we move two pointers, one with speed 1 and another with speed 2, they will end up meet-ing if the linked list has a loop Why? Think about two cars driving on a track—the faster car
will always pass the slower one!
The tricky part here is finding the start of the loop Imagine, as an analogy, two people rac-ing around a track, one running twice as fast as the other If they start off at the same place, when will they next meet? They will next meet at the start of the next lap

Now, let’s suppose Fast Runner had a head start of k meters on an n step lap When will they next meet? They will meet k meters before the start of the next lap (Why? Fast Runner would have made k + 2(n - k) steps, including its head start, and Slow Runner would have made n - k steps Both will be k steps before the start of the loop )
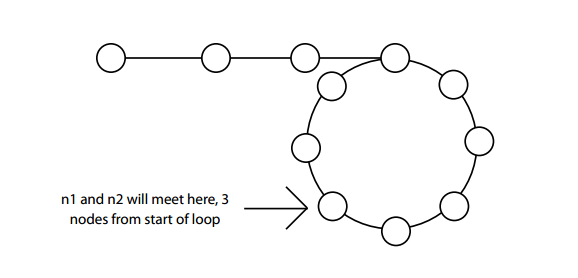
Now, going back to the problem, when Fast Runner (n2) and Slow Runner (n1) are moving around our circular linked list, n2 will have a head start on the loop when n1 enters Specifi-cally, it will have a head start of k, where k is the number of nodes before the loop Since n2 has a head start of k nodes, n1 and n2 will meet k nodes before the start of the loop

So, we now know the following:
1   Head is k nodes from LoopStart (by definition)
2   MeetingPoint for n1 and n2 is k nodes from LoopStart (as shown above)
Thus, if we move n1 back to Head and keep n2 at MeetingPoint, and move them both at the
same pace, they will meet at LoopStart

分析：为何能够找到环的起始位置？

假设环的长度是 m, 进入环前经历的node的个数是 k , 那么，假设经过了时间 t，那么速度为2 的指针距离起始点的位置是:  k + (2t - k) % m = k + (2t - k) - xm . 同理，速度为1的指针距离起始点的位置是 k + (t - k) % m = k + (t - k) - ym。

如果 k + (2t - k) - xm =  k  + (t - k) - ym ，可以得到 t = m (x - y)。 那么当t 最小为m的时候，也就是说，两个指针相聚在 距离 起始点 m - k的环内。换句话说，如果把一个指针移到链表的头部，然后两个指针都以 1 的速度前进，那么它们经过 k 时间后，就可以在环的起始点相遇。

【参考代码】

 1     public static boolean judgeList(LinkList myList)
 2     {
 3         Link fast, slow;
 4         fast = slow = myList.first;
 5         while (true)
 6         {
 7             if (fast == null || fast.next == null)
 8                 return false;
 9             else if (fast == slow || fast.next == slow)
10                 return true;
11             else
12             {
13                 slow = slow.next;
14                 fast = fast.next.next;
15             }
16         }
17     }

 1     public static Link FindBeginning(LinkList myList)
 2     {
 3         Link fast, slow;
 4         fast = slow = myList.first;
 5         while(fast.next !=null)
 6         {
 7             slow = slow.next;
 8             fast = fast.next.next;
 9             if(slow == fast)
10                 break;
11         }
12
13         if(fast.next == null)
14             return null;
15         /* Move slow to Head. Keep fast at Meeting Point. Each are k steps
16         /* from the Loop Start. If they move at the same pace, they must
17          * meet at Loop Start. */
18         slow = myList.first;
19
20         while(slow!=fast)
21         {
22             slow = slow.next;
23             fast = fast.next;
24         }
25
26         return fast;
27     }