lightgbm原理以及Python代码
原论文:
http://papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf
lightgbm原理:
gbdt困点:
gbdt是受欢迎的机器学习算法,当特征维度很高或数据量很大时,有效性和可拓展性没法满足。lightgbm提出GOSS(Gradient-based One-Side Sampling)和EFB(Exclusive Feature Bundling)进行改进。lightgbm与传统的gbdt在达到相同的精确度时,快20倍。
Gradient-based One-Side Sampling (Goss):在GBDT中,数据集没有权重,注意到让不同梯度的数据集在计算信息增益时产生不同的作用。根据信息增益的定义,对于有更大梯度(即训练不足的数据集)将产生更多信息增益。于是,当降低数据集的数据量时,通过保持大梯度的数据集,随机丢掉小梯度的数据集,保持信息增益的准确性。
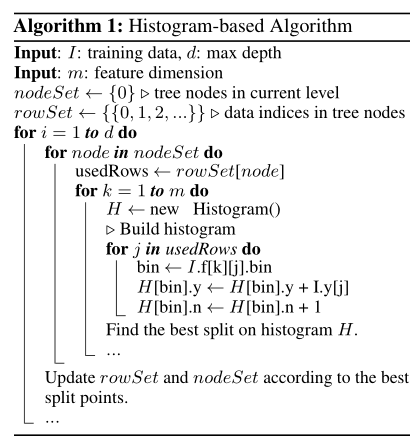

GOSS保持所有具有大梯度的数据集,在小梯度数据集上随机采样。为了抵消对数据分布的影响,GOSS小梯度的样本数据在计算信息增益时引入系数(1-a)/b。具体来说,
- GOSS首先按照数据集的梯度绝对值进行排序,选取最大的a*100%数据集保留;
- 然后从剩余数据集中随机选取b*100%;
- 最后,GOSS对于小梯度乘以常数(1-a)/b放大了样本数据。这样做,我们能不改变原始数据的分布,集中注意力在训练不足的数据上。
收敛分析表明,GOSS算法不会太多降低训练复杂度,并且超越随机选样本。
Exclusive Feature Bundling(EFB). 高维数据通常非常稀疏。特征空间的稀疏性为我们提供了一个设计一种几乎无损的方法来减少特征数量的可能性。具体地说,在一个稀疏的特征空间,许多特征是互斥的,即,它们从不同时取非零值。我们可以安全地将互斥特征捆绑到一个单一的特征中(称之为互斥特征束)。通过精心设计的特征扫描算法,我们可以构建与个体特征类似的基于特征束的特征直方图。这样,直方图构建的复杂性从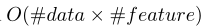 到
到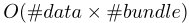 ,其中
,其中 。这样我们可以在不影响准确性情况下大大加快对GBDT的训练。
。这样我们可以在不影响准确性情况下大大加快对GBDT的训练。
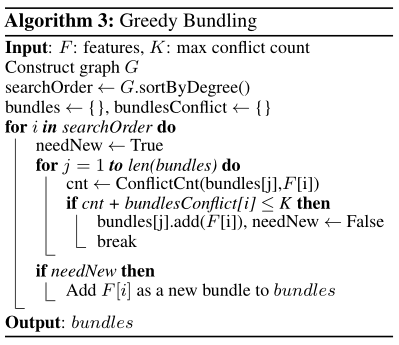

我们的问题对应于图着色问题,反之亦然,因此可以使用贪婪算法来解决。
EFB算法可以将许多互斥性特征捆绑到更少的密集特征上,这可以有效避免了零特征值的不必要计算。事实上,我们也可以通过忽略零特征值,使用表格记录特征非零值的直方图算法。通过扫描表中的数据,直方图构建成本将从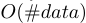 变为
变为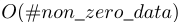 。然而,该方法在树生长过程中需要额外的内存和计算成本来维护这些特征表。我们可以以LightGBM为基本函数按此进行优化。注:这种优化不与EFB冲突,因为我们在捆束稀疏时,依然可以使用它。
。然而,该方法在树生长过程中需要额外的内存和计算成本来维护这些特征表。我们可以以LightGBM为基本函数按此进行优化。注:这种优化不与EFB冲突,因为我们在捆束稀疏时,依然可以使用它。
EFB合并了许多稀疏特征(包括编码特性和隐式互斥性特征),成为少得多的特征。在捆绑过程中包含了基本稀疏特征优化。然而,EFB在树学习过程中为每个特征维护非零数据表,没有额外的成本。更重要的是,因为许多先前孤立的特征被捆绑在一起,它可以增加空间局部性和显著改进缓存命中率。因此,整体效率的提高是引人注目的。以上分析表明,EFB是一种非常有效的在直方图中利用稀疏属性的算法,可以为GBDT训练过程带来显著的加速。
python代码:
import lightgbm
clf=lightgbm
train_matrix = clf.Dataset(tr_x, label=tr_y)
test_matrix = clf.Dataset(te_x, label=te_y)
#z = clf.Dataset(test_x, label=te_y)
#z=test_x
params = {
# 'boosting_type': 'gbdt',
# 'learning_rate': 0.01,
# 'objective': 'binary',
# 'metric': 'auc',
# 'min_child_weight': 1.5,
# 'num_leaves': 2 ** 5,
# 'lambda_l2': 10,
# 'subsample': 0.9,
# 'colsample_bytree': 0.7,
# 'colsample_bylevel': 0.7,
# 'learning_rate': 0.01,
# 'seed': 2017,
# 'nthread': 12,
# 'silent': True,
'task': 'train',
'learning_rate': 0.005,
# 'max_depth': 8,
# 'num_leaves':2**6-1,
'boosting_type': 'gbdt',
'objective': 'binary',
# 'is_unbalance':True,
'feature_fraction': 0.8,
'metric':'auc',
'bagging_fraction': 0.86,
# 'lambda_l1': 0.0001,
'lambda_l2': 49,
'bagging_freq':3,
# 'min_data_in_leaf':5,
'verbose': 1,
'random_state': 2267,
}
num_round = 10000
early_stopping_rounds = 300
if test_matrix:
model = clf.train(params, train_matrix,num_round,valid_sets=test_matrix,
early_stopping_rounds=early_stopping_rounds,verbose_eval=300
)
pre= model.predict(te_x,num_iteration=model.best_iteration).reshape((te_x.shape[0],1))
train[test_index]=pre
test_pre[i, :]= model.predict(test_x, num_iteration=model.best_iteration).reshape((test_x.shape[0],1))
cv_scores.append(roc_auc_score(te_y, pre))
lightgbm原理以及Python代码的更多相关文章
- catboost原理以及Python代码
原论文: http://learningsys.org/nips17/assets/papers/paper_11.pdf catboost原理: One-hot编码可以在预处理阶段或在训练期间 ...
- MD5( 信息摘要算法)的概念原理及python代码的实现
简述: message-digest algorithm 5(信息-摘要算法).经常说的“MD5加密”,就是它→信息-摘要算法. md5,其实就是一种算法.可以将一个字符串,或文件,或压缩包,执行md ...
- KNN算法原理(python代码实现)
kNN(k-nearest neighbor algorithm)算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性 ...
- 【集成学习】:Stacking原理以及Python代码实现
Stacking集成学习在各类机器学习竞赛当中得到了广泛的应用,尤其是在结构化的机器学习竞赛当中表现非常好.今天我们就来介绍下stacking这个在机器学习模型融合当中的大杀器的原理.并在博文的后面附 ...
- 逻辑回归原理(python代码实现)
Logistic Regression Classifier逻辑回归主要思想就是用最大似然概率方法构建出方程,为最大化方程,利用牛顿梯度上升求解方程参数. 优点:计算代价不高,易于理解和实现. 缺点: ...
- 【机器学习】:Kmeans均值聚类算法原理(附带Python代码实现)
这个算法中文名为k均值聚类算法,首先我们在二维的特殊条件下讨论其实现的过程,方便大家理解. 第一步.随机生成质心 由于这是一个无监督学习的算法,因此我们首先在一个二维的坐标轴下随机给定一堆点,并随即给 ...
- paip.输入法编程--英文ati化By音标原理与中文atiEn处理流程 python 代码为例
paip.输入法编程--英文ati化By音标原理与中文atiEn处理流程 python 代码为例 #---目标 1. en vs enPHati 2.en vs enPhAtiSmp 3.cn vs ...
- 决策树ID3原理及R语言python代码实现(西瓜书)
决策树ID3原理及R语言python代码实现(西瓜书) 摘要: 决策树是机器学习中一种非常常见的分类与回归方法,可以认为是if-else结构的规则.分类决策树是由节点和有向边组成的树形结构,节点表示特 ...
- 模拟退火算法SA原理及python、java、php、c++语言代码实现TSP旅行商问题,智能优化算法,随机寻优算法,全局最短路径
模拟退火算法SA原理及python.java.php.c++语言代码实现TSP旅行商问题,智能优化算法,随机寻优算法,全局最短路径 模拟退火算法(Simulated Annealing,SA)最早的思 ...
随机推荐
- vector,deque,list的区别和使用
vector: 表示一段连续的内存区域,每个元素被顺序存储在这段内存中,对vector的随机访问效率很高,但对非末尾元素的插入和删除则效率非常低. deque: 也表示N段连续的内存区域组成,但与ve ...
- httpclient介绍与使用
什么是httpclient HttpClient 是 Apache Jakarta Common 下的子项目,用来提供高效的.最新的.功能丰富的支持 HTTP 协议的客户端编程工具包,并且它支持 HT ...
- haproxy [WARNING] 312/111530 (17395) : config : 'option forwardfor' ignored for frontend 'harbor_login' as it requires HTTP mode.
1.经过调查, 2down voteaccepted x-forwarded-for is an HTTP header field, so has nothing to do with the tr ...
- (四)Lua脚本语言入门(数组遍历)
这篇文章就当成铺垫型的文章,写着写着发现有好多想写的,,关于C#与Java,当然作为铺垫肯定与Lua的下部分介绍有关..... 对于"泛型",先看C#中"泛型" ...
- Oracle 批量修改某个用户下表的表空间
说明:一般来说要修改表的表空间需要同时修改表的表空间和其对应的索引表空间,并且在修改含有BOLB字段的表的表空间时又不一样,具体请参考末尾的链接 思路:拼凑一个满足条件的批处理查询语句,将查询的结果复 ...
- 写个定时任务更新svn
最近学了点shell编程,寻思锻炼下写一个.平常你学习或者看别人讲,自己不练习肯定不行,基本上一动手准出错哈哈.等自己去实践,才会知道哪里有问题,哪里容易出错,哪里要注意什么的. 因为我们每个人有自己 ...
- 将jar文件加到Maven的local repository中
对于Maven项目来说,日常使用的多数第三方java库文件都可以从Maven的Central Repository中自动下载,但是如果我们需要的jar文件不在Central Repository中,那 ...
- 20155204 王昊《网络对抗技术》EXP4
20155204 王昊<网络对抗技术>EXP4 一.实验后回答问题 (1)如果在工作中怀疑一台主机上有恶意代码,但只是猜想,所有想监控下系统一天天的到底在干些什么.请设计下你想监控的操作有 ...
- Luogu P4071 [SDOI2016]排列计数
晚上XZTdalao给我推荐了这道数论题.太棒了又可以A一道省选题了 其实这道题也就考一个错排公式+组合数+乘法逆元 我们来一步一步分析 错排公式 通俗的说就是把n个1~n的数排成一个序列A,并使得所 ...
- Package 设计3:数据源的提取和使用暂存
SSIS 设计系列: Package设计1:选择数据类型.暂存数据和并发 Package设计2:增量更新 Package 设计3:数据源的提取和使用暂存 在使用SSIS Package处理海量数据时, ...
