kmeans理解

最近看到Andrew Ng的一篇论文，文中用到了Kmeans和DL结合的思想，突然发现自己对ML最基本的聚类算法都不清楚，于是着重的看了下Kmeans，并在网上找了程序跑了下。

kmeans是unsupervised learning最基本的一个聚类算法，我们可以用它来学习无标签的特征，其基本思想如下：

首先给出原始数据{x1,x2,...,xn}，这些数据没有被标记的。

初始化k个随机数据u1,u2,...,uk，每一个ui都是一个聚类中心，k就是分为k类，这些xn和uk都是向量。

根据下面两个公式迭代就能求出最终所有的聚类中心u。

formula 1：

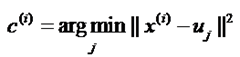
其中xi是第i个data，uj是第j（1~k）的聚类中心，这个公式的意思就是求出每一个data到k个聚类中心的距离，并求出最小距离，那么数据xi就可以归到这一类。

formula 2：

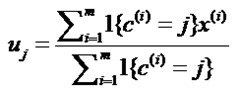
这个公式的目的是求出新的聚类中心，由于之前已经求出来每一个data到每一类的聚类中心uj，那么可以在每一类总求出其新的聚类中心（用这一类每一个data到中心的距离之和除以总的data），分别对k类同样的处理，这样我们就得到了k个新的聚类中心。

反复迭代公式一和公式二，知道聚类中心不怎么改变为止。

我们利用3维数据进行kmeans，代码如下：

run_means.m

   1: %%用来kmeans聚类的一个小代码

   2:  

   3: clear all;

   4: close all;

   5: clc;

   6:  

   7: %第一类数据

   8: mu1=[0 0 0];  %均值

   9: S1=[0.3 0 0;0 0.35 0;0 0 0.3];  %协方差

  10: data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据

  11:  

  12: %%第二类数据

  13: mu2=[1.25 1.25 1.25];

  14: S2=[0.3 0 0;0 0.35 0;0 0 0.3];

  15: data2=mvnrnd(mu2,S2,100);

  16:  

  17: %第三个类数据

  18: mu3=[-1.25 1.25 -1.25];

  19: S3=[0.3 0 0;0 0.35 0;0 0 0.3];

  20: data3=mvnrnd(mu3,S3,100);

  21:  

  22: %显示数据

  23: plot3(data1(:,1),data1(:,2),data1(:,3),'+');

  24: hold on;

  25: plot3(data2(:,1),data2(:,2),data2(:,3),'r+');

  26: plot3(data3(:,1),data3(:,2),data3(:,3),'g+');

  27: grid on;

  28:  

  29: %三类数据合成一个不带标号的数据类

  30: data=[data1;data2;data3];   %这里的data是不带标号的

  31:  

  32: %k-means聚类

  33: [u re]=KMeans(data,3);  %最后产生带标号的数据，标号在所有数据的最后，意思就是数据再加一维度

  34: [m n]=size(re);

  35:  

  36: %最后显示聚类后的数据

  37: figure;

  38: hold on;

  39: for i=1:m 

  40:     if re(i,4)==1   

  41:          plot3(re(i,1),re(i,2),re(i,3),'ro'); 

  42:     elseif re(i,4)==2

  43:          plot3(re(i,1),re(i,2),re(i,3),'go'); 

  44:     else 

  45:          plot3(re(i,1),re(i,2),re(i,3),'bo'); 

  46:     end

  47: end

  48: grid on;

KMeans.m

   1: %N是数据一共分多少类

   2: %data是输入的不带分类标号的数据

   3: %u是每一类的中心

   4: %re是返回的带分类标号的数据

   5: function [u re]=KMeans(data,N)   

   6:     [m n]=size(data);   %m是数据个数，n是数据维数

   7:     ma=zeros(n);        %每一维最大的数

   8:     mi=zeros(n);        %每一维最小的数

   9:     u=zeros(N,n);       %随机初始化，最终迭代到每一类的中心位置

  10:     for i=1:n

  11:        ma(i)=max(data(:,i));    %每一维最大的数

  12:        mi(i)=min(data(:,i));    %每一维最小的数

  13:        for j=1:N

  14:             u(j,i)=ma(i)+(mi(i)-ma(i))*rand();  %随机初始化，不过还是在每一维[min max]中初始化好些

  15:        end      

  16:     end

  17:    

  18:     while 1

  19:         pre_u=u;            %上一次求得的中心位置

  20:         for i=1:N

  21:             tmp{i}=[];      % 公式一中的x(i)-uj,为公式一实现做准备

  22:             for j=1:m

  23:                 tmp{i}=[tmp{i};data(j,:)-u(i,:)];

  24:             end

  25:         end

  26:         

  27:         quan=zeros(m,N);

  28:         for i=1:m        %公式一的实现

  29:             c=[];        %c 是到每类的距离

  30:             for j=1:N

  31:                 c=[c norm(tmp{j}(i,:))];

  32:             end

  33:             [junk index]=min(c);

  34:             quan(i,index)=norm(tmp{index}(i,:));           

  35:         end

  36:         

  37:         for i=1:N            %公式二的实现

  38:            for j=1:n

  39:                 u(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));

  40:            end           

  41:         end

  42:         

  43:         if norm(pre_u-u)<0.1  %不断迭代直到位置不再变化

  44:             break;

  45:         end

  46:     end

  47:     

  48:     re=[];

  49:     for i=1:m

  50:         tmp=[];

  51:         for j=1:N

  52:             tmp=[tmp norm(data(i,:)-u(j,:))];

  53:         end

  54:         [junk index]=min(tmp);

  55:         re=[re;data(i,:) index];

  56:     end

  57:     

  58: end

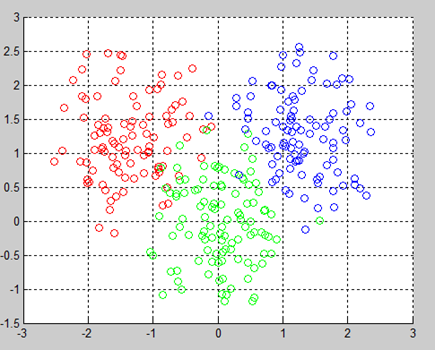
原始数据如下所示，分为三类：

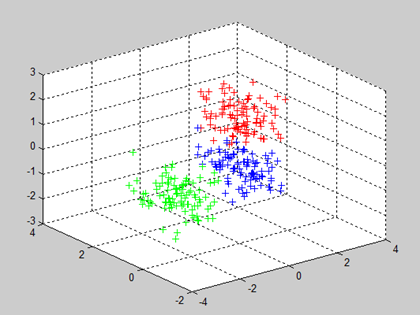
当k取2时，聚成2类：

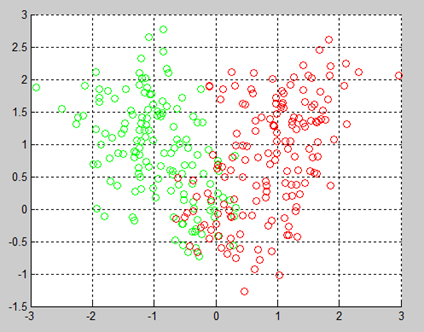
当k取3时，聚成3类：