Project Euler 100 : Arranged probability 安排概率

Arranged probability

If a box contains twenty-one coloured discs, composed of fifteen blue discs and six red discs, and two discs were taken at random, it can be seen that the probability of taking two blue discs, P(BB) = (15/21)×(14/20) = 1/2.

The next such arrangement, for which there is exactly 50% chance of taking two blue discs at random, is a box containing eighty-five blue discs and thirty-five red discs.

By finding the first arrangement to contain over 1012 = 1,000,000,000,000 discs in total, determine the number of blue discs that the box would contain.

---

安排概率

在一个盒子中装有21个彩色碟子，其中15个是蓝的，6个是红的。如果随机地从盒子中取出两个碟子，取出两个蓝色碟子的概率是P(BB) = (15/21)×(14/20) = 1/2。

下一组使得取出两个蓝色盘子的概率恰好为50%的安排，是在盒子中装有85个蓝色碟子和35个红色碟子。

当盒子中装有超过10¹² = 1,000,000,000,000个碟子时，找出第一组满足上述要求的安排，并求此时盒子中蓝色碟子的数量。

解题

表示暴力破解不可以。

昨天晚上10点开始跑，到今天15.30还没有出来结果，跑到了下面的结果：

然而正确答案时候的碟子总数是：

1070379110497

Python

# coding=gbk
 
import time as time
import re
import math
def run():
    n = 10**12
    MAX = 10**16
    index = 0
    while n<MAX:
        x = solvex(n)
        if x!=0:
            print x
            break
        n+=1
        index+=1
        if index%1000000==0:
            print n 
 
def solvex(n):
    dlt = delt(n)
    if judge(dlt):
        x = 1 + int(dlt**0.5)
        if x%2==0:
            return x/2
    return 0 
 
def judge(dlt):
    sq = int(dlt**0.5)
    return sq**2 == dlt 
 
def delt(n):
    dlt = 2*n*(n-1)
    return dlt
 
t0 = time.time()
run()
t1 = time.time()
print "running time=",(t1-t0),"s"

这个博客多长提到，里面提到一个链接

设总的碟子数是x，蓝色碟子数是y

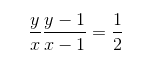
化简为：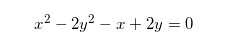

第二个链接中给了求解方法

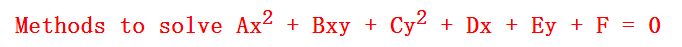
对于一般的二次方程的解是：

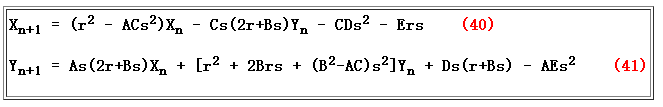
对这一题而言：

A=1

B=0
C=-2
D=-1

E=2

F=0

r=3 s =2 带入求解

def run():
    MAX = 10**12
    x = 21
    y = 15
    while x<MAX:
        print x,y
        tmpx = 17*x + 24*y -20
        tmpy = 12*x + 17*y -14
        x = tmpx
        y = tmpy
 
    print x, y 

但是这里的输出结果只是部分答案，但是我们要的答案还在里面。

21 15
697 493
23661 16731
803761 568345
27304197 19306983
927538921 655869061
31509019101 22280241075
1070379110497 756872327473

上面第一个链接好像应该是这样来的：

r = 3 s =2计算PEQS

上面的r s 应该是r1 s1 这样反过来再去 r s 好像就和上面博客中的一样了。。。。。

def run():
    MAX = 10**12
    x = 21
    y = 15
    while x<MAX:
        print x,y
        tmpy = 3*y+2*x-2
        tmpx = 4*y+3*x-3
        x = tmpx
        y = tmpy
    print x,y  

输出结果是

21 15
120 85
697 493
4060 2871
23661 16731
137904 97513
803761 568345
4684660 3312555
27304197 19306983
159140520 112529341
927538921 655869061
5406093004 3822685023
31509019101 22280241075
183648021600 129858761425
1070379110497 756872327473

然而在这个中文博客中直接没有考虑常数项，xy初始值变成了1

JAVA

package Level3;
 
public class PE0100{
    public static void run(){
        long MAX = 1000000;
        long x = 21;
        long y = 15;
        while(x/MAX<MAX){
            long tmpx = 4*y+3*x -3;
            long tmpy = 3*y+2*x -2;
            x = tmpx;
            y = tmpy;
        }
        System.out.println(y);
 
    }
    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        run();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");
 
    }
}