最长公共子序列LCS

LCS：给出两个序列S1和S2，求出的这两个序列的最大公共部分S3就是就是S1和S2的最长公共子序列了。公共部分

必须是以相同的顺序出现，但是不必要是连续的。

LCS具有最优子结构，且满足重叠子问题的性质。所以我们可以用动态规划来解决LCS问题。

由LCS问题的最优子结构可得出递归式：

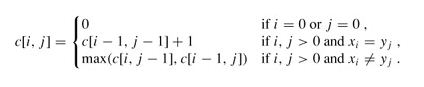
长度的问题我们已经解决了，这次要解决输出最长子序列的问题，

我们采用一个标记函数Flag[i,j]，当

①：C[i,j]=C[i-1,j-1]+1  时 标记Flag[i,j]="left_up";    （左上方箭头）

②：C[i-1,j]>=C[i,j-1]   时 标记Flag[i,j]="left";          （左箭头）

③: C[i-1,j]<C[i,j-1]     时 标记Flag[i,j]="up";            （上箭头）

例如：我输入两个序列X=acgbfhk，Y=cegefkh。

 1 using System;
 2
 3 namespace ConsoleApplication2
 4 {
 5     public class Program
 6     {
 7         static int[,] martix;
 8
 9         static string[,] flag;
10
11         static string str1 = "acgbfhk";
12
13         static string str2 = "cegefkh";
14
15         static void Main(string[] args)
16         {
17             martix = new int[str1.Length + 1, str2.Length + 1];
18
19             flag = new string[str1.Length + 1, str2.Length + 1];
20
21             LCS(str1, str2);
22
23             //打印子序列
24             SubSequence(str1.Length, str2.Length);
25
26             Console.Read();
27         }
28
29         static void LCS(string str1, string str2)
30         {
31             //初始化边界，过滤掉0的情况
32             for (int i = 0; i <= str1.Length; i++)
33                 martix[i, 0] = 0;
34
35             for (int j = 0; j <= str2.Length; j++)
36                 martix[0, j] = 0;
37
38             //填充矩阵
39             for (int i = 1; i <= str1.Length; i++)
40             {
41                 for (int j = 1; j <= str2.Length; j++)
42                 {
43                     //相等的情况
44                     if (str1[i - 1] == str2[j - 1])
45                     {
46                         martix[i, j] = martix[i - 1, j - 1] + 1;
47                         flag[i, j] = "left_up";
48                     }
49                     else
50                     {
51                         //比较“左边”和“上边“，根据其max来填充
52                         if (martix[i - 1, j] >= martix[i, j - 1])
53                         {
54                             martix[i, j] = martix[i - 1, j];
55                             flag[i, j] = "left";
56                         }
57                         else
58                         {
59                             martix[i, j] = martix[i, j - 1];
60                             flag[i, j] = "up";
61                         }
62                     }
63                 }
64             }
65         }
66
67         static void SubSequence(int i, int j)
68         {
69             if (i == 0 || j == 0)
70                 return;
71
72             if (flag[i, j] == "left_up")
73             {
74                 Console.WriteLine("{0}: 当前坐标:（{1},{2}）", str2[j - 1], i - 1, j - 1);
75
76                 //左前方
77                 SubSequence(i - 1, j - 1);
78             }
79             else
80             {
81                 if (flag[i, j] == "up")
82                 {
83                     SubSequence(i, j - 1);
84                 }
85                 else
86                 {
87                     SubSequence(i - 1, j);
88                 }
89             }
90         }
91     }
92 }

由于直接绘图很麻烦，嘿嘿，我就用手机拍了张：

好，我们再输入两个字符串：

1         static string str1 = "abcbdab";
2
3         static string str2 = "bdcaba";

通过上面的两张图，我们来分析下它的时间复杂度和空间复杂度。

时间复杂度：构建矩阵我们花费了O(MN)的时间，回溯时我们花费了O（M+N)的时间，两者相加最终我们花费了O(MN)的时间。

空间复杂度：构建矩阵我们花费了O(MN)的空间，标记函数也花费了O(MN)的空间，两者相加最终我们花费了O(MN)的空间。