[HNOI 2004]敲砖块

Description

在一个凹槽中放置了 n 层砖块、最上面的一层有n 块砖，从上到下每层依次减少一块砖。每块砖都有一个分值，敲掉这块砖就能得到相应的分值，如下图所示。

14 15  4  3  23

 33  33 76  2

   2   13 11

     22 23

       31

如果你想敲掉第 i 层的第j 块砖的话，若i=1，你可以直接敲掉它；若i>1，则你必须先敲掉第i-1 层的第j 和第j+1 块砖。

你现在可以敲掉最多 m 块砖，求得分最多能有多少。

Input

输入文件的第一行为两个正整数 n 和m；接下来n 行，描述这n 层砖块上的分值a[i][j],满足0≤a[i][j]≤100。

对于 100%的数据，满足1≤n≤50，1≤m≤n*(n+1)/2；

Output

输出文件仅一行为一个正整数，表示被敲掉砖块的最大价值总和。

Sample Input

4 5
2 2 3 4
8 2 7
2 3
49

Sample Output

题解

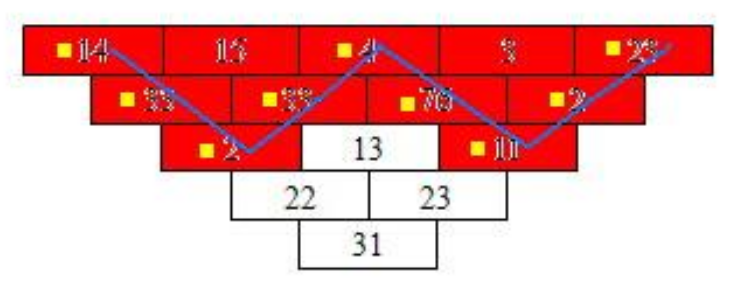
分析题目中的选取条件,我们会发现:
这道题最终解的形态(选中的数字)可以描述成若干个三角形相互连接或重叠,如上图中的红色砖块,由两个蓝色标识的三角形部分重叠而成。
将最终解的形态(选中的数字)的每列最下层点用线画出(图中的蓝线),可以发现:
1、构成的轮廓线是一条锯齿状的折线;
2、轮廓线上的相邻点布局在三角形的相列与相邻行上,即如果从左向右观察列,轮廓线上的点只能从其左列的上方行或下方行连过来;
3、轮廓线上点所在列的上方点一定全部被选中。
则把原问题转化为沟画出重叠三角形的锯齿状轮廓折线,找到一条合法的路径,使得围在轮廓线内的数字代价和最大。
另,根据第 3 点分析,轮廓线上点所在列的上方点一定全部被选中,可将选中的数字压缩到轮廓线上点,问题进一步转化为求轮廓线上点的代价和最大。

算法

1、预处理:设 $cost[i,j]$表示选取第 $i$ 行第 $j$ 个,需要一起选取的其他点的个数。即与这个点同一列,且在这个点之上的点的个数。
2、$sum[i,j]$表示选取第 $i$ 行第 $j$ 个,需要一起选取的其他点的数值和。即与这个点同一列,且在这个点之上的点的数值之和。这样,$cost[]$,$sum[]$分别记录了走到每个格子本列的数字个数与代价和。
3、因为对于任意一列的任意一个数字,转移到它的前提与之前的方案无关,所以满足了$dp$ 的无后效性。同时当前列必定要由之前的某个最优状态转移过来,所以又满足了最优子结构的性质。故 $DP$ 是可行的。

 //It is made by Awson on 2017.10.31

 #include <set>

 #include <map>

 #include <cmath>

 #include <ctime>

 #include <queue>

 #include <stack>

 #include <vector>

 #include <cstdio>

 #include <string>

 #include <cstdlib>

 #include <cstring>

 #include <iostream>

 #include <algorithm>

 #define LL long long

 #define Max(a, b) ((a) > (b) ? (a) : (b))

 #define Min(a, b) ((a) < (b) ? (a) : (b))

 using namespace std;

 int n, m;

 int mp[][], cnt[][];

 int f[][][];

 void work() {

     scanf("%d%d", &n, &m);

     for (int i = ; i <= n; i++) for (int j = ; j <= n-i+; j++) scanf("%d", &mp[i][j]);

     for (int i = ; i <= n; i++)

     for (int j = ; j <= n-i+; j++) {

         if (i- >= ) mp[i][j] += mp[i-][j+];

         cnt[i][j] = (i+)/;

     }

     memset(f, -, sizeof(f));

     f[][][] = ; f[][][] = mp[][];

     for (int y = ; y <= n; y++)

     for (int x = ; x <= n-y+; x++)

         for (int k = ; k <= m; k++)

         if (f[x][y][k] != -) {

             f[x+][y][k+cnt[x+][y]] = Max(f[x+][y][k+cnt[x+][y]], f[x][y][k]+mp[x+][y]);

             if (x == ) f[x][y+][k] = Max(f[x][y+][k], f[x][y][k]);

             else f[x-][y+][k+cnt[x-][y+]] = Max(f[x-][y+][k+cnt[x-][y+]], f[x][y][k]+mp[x-][y+]);

         }

     printf("%d\n", f[][n+][m]);

 }

 int main() {

     work();

     return ;

 }