决策树系列（四）——C4.5
如上一篇文章所述，ID3方法主要有几个缺点：一是采用信息增益进行数据分裂，准确性不如信息增益率；二是不能对连续数据进行处理，只能通过连续数据离散化进行处理；三是没有采用剪枝的策略，决策树的结构可能会过于复杂，可能会出现过拟合的情况。
C4.5在ID3的基础上对上述三个方面进行了相应的改进：
a） C4.5对节点进行分裂时采用信息增益率作为分裂的依据；
b） 能够对连续数据进行处理；
c） C4.5采用剪枝的策略，对完全生长的决策树进行剪枝处理，一定程度上降低过拟合的影响。
1.采用信息增益率作为分裂的依据
信息增益率的计算公式为：
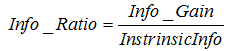
其中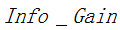
表示信息增益，
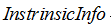表示分裂子节点数据量的信息增益，计算公式为：
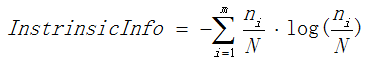
其中m表示节点的数量，Ni表示第i个节点的数据量，N表示父亲节点的数据量，说白了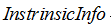，其实是分裂节点的熵。
信息增益率越大，说明分裂的效果越好。
以一个实际的例子说明C4.5如何通过信息增益率选择分裂的属性：
表1 原始数据表
|
当天天气 |
温度 |
湿度 |
日期 |
逛街 |
|
晴 |
25 |
50 |
工作日 |
否 |
|
晴 |
21 |
48 |
工作日 |
是 |
|
晴 |
18 |
70 |
周末 |
是 |
|
晴 |
28 |
41 |
周末 |
是 |
|
阴 |
8 |
65 |
工作日 |
是 |
|
阴 |
18 |
43 |
工作日 |
否 |
|
阴 |
24 |
56 |
周末 |
是 |
|
阴 |
18 |
76 |
周末 |
否 |
|
雨 |
31 |
61 |
周末 |
否 |
|
雨 |
6 |
43 |
周末 |
是 |
|
雨 |
15 |
55 |
工作日 |
否 |
|
雨 |
4 |
58 |
工作日 |
否 |
以当天天气为例：
一共有三个属性值，晴、阴、雨，一共分裂成三个子节点。
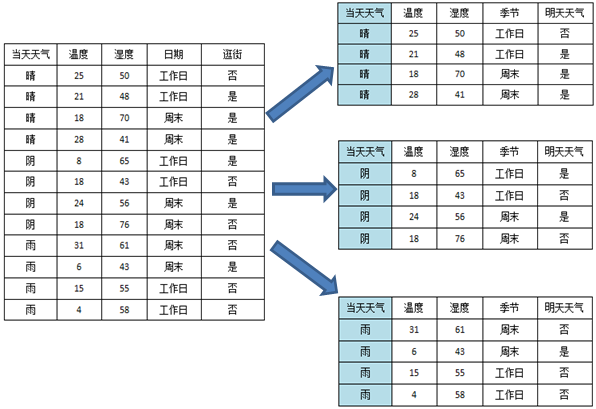
根据上述公式，可以计算信息增益率如下：
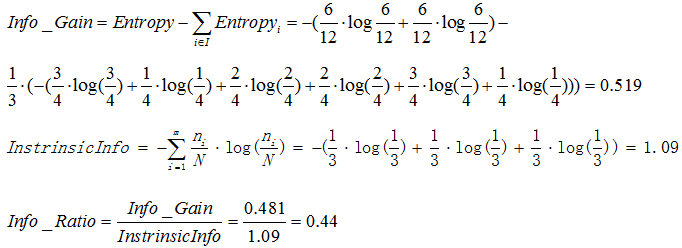
所以使用天气属性进行分裂可以得到信息增益率0.44。
2.对连续型属性进行处理
C4.5处理离散型属性的方式与ID3一致，新增对连续型属性的处理。处理方式是先根据连续型属性进行排序，然后采用一刀切的方式将数据砍成两半。
那么如何选择切割点呢？很简单，直接计算每一个切割点切割后的信息增益，然后选择使分裂效果最优的切割点。以温度为例：
从上图可以看出，理论上来讲，N条数据就有N-1个切割点，为了选取最优的切割垫，要计算按每一次切割的信息增益，计算量是比较大的，那么有没有简化的方法呢？有，注意到，其实有些切割点是很明显可以排除的。比如说上图右侧的第2条和第3条记录，两者的类标签（逛街）都是“是”，如果从这里切割的话，就将两个本来相同的类分开了，肯定不会比将他们归为一类的切分方法好，因此，可以通过去除前后两个类标签相同的切割点以简化计算的复杂度，如下图所示：
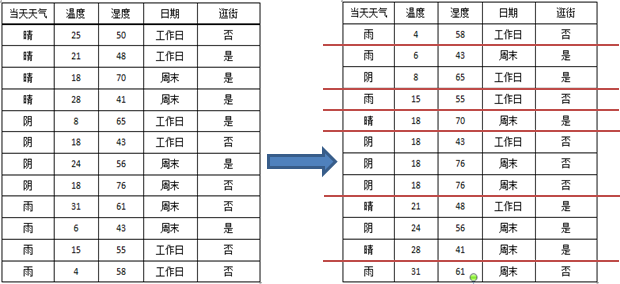
从图中可以看出，最终切割点的数目从原来的11个减少到现在的6个，降低了计算的复杂度。
确定了分割点之后，接下来就是选择最优的分割点了，注意，对连续型属性是采用信息增益进行内部择优的，因为如果使用信息增益率进行分裂会出现倾向于选择分割前后两个节点数据量相差最大的分割点，为了避免这种情况，选择信息增益选择分割点。选择了最优的分割点之后，再计算信息增益率跟其他的属性进行比较，确定最优的分裂属性。
3. 剪枝
决策树只已经提到，剪枝是在完全生长的决策树的基础上，对生长后分类效果不佳的子树进行修剪，减小决策树的复杂度，降低过拟合的影响。
C4.5采用悲观剪枝方法（PEP）。悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话，则进行剪枝。怎样才算是没有影响？如果剪枝后的误差小于剪枝前经度的上限，则说明剪枝后的效果与更佳，此时需要子树进行剪枝操作。
进行剪枝必须满足的条件：
其中：
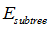表示子树的误差；
表示叶子节点的误差；
令子树误差的经度满足二项分布，根据二项分布的性质，
，
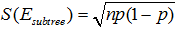，其中
，N为子树的数据量；同样，叶子节点的误差
。
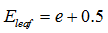上述公式中，0.5表示修正因子。由于对父节点进行分裂总会得到比父节点分类结果更好的效果，因此，因此从理论上来说，父节点的误差总是不小于孩子节点的误差，因此需要进行修正，给每一个节点都加上0.5的修正因此，在计算误差的时候，子节点由于加上了修正的因子，就无法保证总误差总是低于父节点。
算例：
由于
，所以应该进行剪枝。
程序设计及源代码（C#版）
程序的设计过程
（1）数据格式
对原始的数据进行数字化处理，并以二维数据的形式存储，每一行表示一条记录，前n-1列表示属性，最后一列表示分类的标签。
如表1的数据可以转化为表2：
表2 初始化后的数据
|
当天天气 |
温度 |
湿度 |
季节 |
明天天气 |
|
1 |
25 |
50 |
1 |
1 |
|
2 |
21 |
48 |
1 |
2 |
|
2 |
18 |
70 |
1 |
3 |
|
1 |
28 |
41 |
2 |
1 |
|
3 |
8 |
65 |
3 |
2 |
|
1 |
18 |
43 |
2 |
1 |
|
2 |
24 |
56 |
4 |
1 |
|
3 |
18 |
76 |
4 |
2 |
|
3 |
31 |
61 |
2 |
1 |
|
2 |
6 |
43 |
3 |
3 |
|
1 |
15 |
55 |
4 |
2 |
|
3 |
4 |
58 |
3 |
3 |
其中，对于“当天天气”属性，数字{1，2，3}分别表示{晴，阴，雨}；对于“季节”属性{1，2，3，4}分别表示{春天、夏天、冬天、秋天}；对于类标签“明天天气”，数字{1，2，3}分别表示{晴、阴、雨}。
代码如下所示：
static double[][] allData; //存储进行训练的数据
static List<String>[] featureValues; //离散属性对应的离散值
featureValues是链表数组，数组的长度为属性的个数，数组的每个元素为该属性的离散值链表。
（2）两个类：节点类和分裂信息
a）节点类Node
该类表示一个节点，属性包括节点选择的分裂属性、节点的输出类、孩子节点、深度等。注意，与ID3中相比，新增了两个属性：leafWrong和leafNode_Count分别表示叶子节点的总分类误差和叶子节点的个数，主要是为了方便剪枝。
class Node
{
/// <summary>
/// 各个子节点对应的取值
/// </summary>
//public List<String> features;
public List<String> features{get;set;}
/// <summary>
/// 分裂属性的数据类型（1：连续 0：离散）
/// </summary>
public String feature_Type {get;set;}
/// <summary>
/// 分裂属性列的下标
/// </summary>
public String SplitFeature {get;set;}
/// <summary>
/// 各类别的数量统计
/// </summary>
public double[] ClassCount {get;set;}
/// <summary>
/// 数据量
/// </summary>
public int rowCount { get; set; }
/// <summary>
/// 各个子节点
/// </summary>
public List<Node> childNodes {get;set;}
/// <summary>
/// 父亲节点
/// </summary>
public Node Parent {get;set;}
/// <summary>
/// 该节点占比最大的类别
/// </summary>
public String finalResult {get;set;}
/// <summary>
/// 数的深度
/// </summary>
public int deep {get;set;}
/// <summary>
/// 节点占比最大类的标号
/// </summary>
public int result {get;set;}
/// <summary>
/// 子节点的错误数
/// </summary>
public int leafWrong {get;set;}
/// <summary>
/// 子节点的数目
/// </summary>
public int leafNode_Count {get;set;} public double getErrorCount()
{
return rowCount - ClassCount[result];
}
#region
public void setClassCount(double[] count)
{
this.ClassCount = count;
double max = ClassCount[];
int result = ;
for (int i = ; i < ClassCount.Length; i++)
{
if (max < ClassCount[i])
{
max = ClassCount[i];
result = i;
}
}
this.result = result;
}
#endregion
}
b）分裂信息类，该类存储节点进行分裂的信息，包括各个子节点的行坐标、子节点各个类的数目、该节点分裂的属性、属性的类型等。
class SplitInfo
{
/// <summary>
/// 分裂的属性下标
/// </summary>
public int splitIndex { get; set; }
/// <summary>
/// 数据类型
/// </summary>
public int type { get; set; }
/// <summary>
/// 分裂属性的取值
/// </summary>
public List<String> features { get; set; }
/// <summary>
/// 各个节点的行坐标链表
/// </summary>
public List<int>[] temp { get; set; }
/// <summary>
/// 每个节点各类的数目
/// </summary>
public double[][] class_Count { get; set; }
}
主方法findBestSplit(Node node,List<int> nums,int[] isUsed)，该方法对节点进行分裂
其中：
node表示即将进行分裂的节点；
nums表示节点数据的行坐标列表；
isUsed表示到该节点位置所有属性的使用情况；
findBestSplit的这个方法主要有以下几个组成部分：
1）节点分裂停止的判定
节点分裂条件如上文所述，源代码如下：
public static bool ifEnd(Node node, double entropy,int[] isUsed)
{
try
{
double[] count = node.ClassCount;
int rowCount = node.rowCount;
int maxResult = ;
#region 数达到某一深度
int deep = node.deep;
if (deep >= maxDeep)
{
maxResult = node.result + ;
node.feature_Type=("result");
node.features=(new List<String>() { maxResult + "" });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 纯度(其实跟后面的有点重了，记得要修改)
//maxResult = 1;
//for (int i = 1; i < count.Length; i++)
//{
// if (count[i] / rowCount >= 0.95)
// {
// node.feature_Type=("result");
// node.features=(new List<String> { "" + (i + 1) });
// node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1]));
// node.leafNode_Count = 1;
// return true;
// }
//}
#endregion
#region 熵为0
if (entropy == )
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { maxResult + "" });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 属性已经分完
bool flag = true;
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
flag = false;
break;
}
}
if (flag)
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 数据量少于100
if (rowCount < Limit_Node)
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
return false;
}
catch (Exception e)
{
return false;
}
}
2）寻找最优的分裂属性
寻找最优的分裂属性需要计算每一个分裂属性分裂后的信息增益率，计算公式上文已给出，其中熵的计算代码如下：
public static double CalEntropy(double[] counts, int countAll)
{
try
{
double allShang = ;
for (int i = ; i < counts.Length; i++)
{
if (counts[i] == )
{
continue;
}
double rate = counts[i] / countAll;
allShang = allShang + rate * Math.Log(rate, );
}
return allShang;
}
catch (Exception e)
{
return ;
}
}
3）进行分裂，同时对子节点进行迭代处理
其实就是递归的工程，对每一个子节点执行findBestSplit方法进行分裂。
findBestSplit源代码：
public static Node findBestSplit(Node node, List<int> nums, int[] isUsed)
{
try
{
//判断是否继续分裂
double totalShang = CalEntropy(node.ClassCount, node.rowCount);
if (ifEnd(node, totalShang,isUsed))
{
return node;
}
#region 变量声明
SplitInfo info = new SplitInfo();
int RowCount = nums.Count; //样本总数
double jubuMax = ; //局部最大熵
#endregion
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
continue;
}
#region 离散变量
if (type[i] == )
{
int[] allFeatureCount = new int[]; //所有类别的数量
double[][] allCount = new double[allNum[i]][];
for (int j = ; j < allCount.Length; j++)
{
allCount[j] = new double[classCount];
}
int[] countAllFeature = new int[allNum[i]];
List<int>[] temp = new List<int>[allNum[i]];
for (int j = ; j < temp.Length; j++)
{
temp[j] = new List<int>();
}
for (int j = ; j < nums.Count; j++)
{
int index = Convert.ToInt32(allData[nums[j]][i]);
temp[index - ].Add(nums[j]);
countAllFeature[index - ]++;
allCount[index - ][Convert.ToInt32(allData[nums[j]][lieshu - ]) - ]++;
}
double allShang = ;
double chushu = ;
for (int j = ; j < allCount.Length; j++)
{
allShang = allShang + CalEntropy(allCount[j], countAllFeature[j]) * countAllFeature[j] / RowCount;
if (countAllFeature[j] > )
{
double rate = countAllFeature[j] / Convert.ToDouble(RowCount);
chushu = chushu + rate * Math.Log(rate, );
}
}
allShang = (-totalShang + allShang);
if (allShang > jubuMax)
{
info.features = new List<string>();
info.type = ;
info.temp = temp;
info.splitIndex = i;
info.class_Count = allCount;
jubuMax = allShang;
allFeatureCount = countAllFeature;
}
}
#endregion
#region 连续变量
else
{
double[] leftCount = new double[classCount]; //做节点各个类别的数量
double[] rightCount = new double[classCount]; //右节点各个类别的数量
double[] count1 = new double[classCount]; //子集1的统计量
//double[] count2 = new double[node.getCount().Length]; //子集2的统计量
double[] count2 = new double[node.ClassCount.Length]; //子集2的统计量
for (int j = ; j < node.ClassCount.Length; j++)
{
count2[j] = node.ClassCount[j];
}
int all1 = ; //子集1的样本量
int all2 = nums.Count; //子集2的样本量
double lastValue = ; //上一个记录的类别
double currentValue = ; //当前类别
double lastPoint = ; //上一个点的值
double currentPoint = ; //当前点的值
int splitPoint = ;
double splitValue = ;
double[] values = new double[nums.Count];
for (int j = ; j < values.Length; j++)
{
values[j] = allData[nums[j]][i];
}
QSort(values, nums, , nums.Count - );
double chushu = ;
double lianxuMax = ; //连续型属性的最大熵
for (int j = ; j < nums.Count - ; j++)
{
currentValue = allData[nums[j]][lieshu - ];
currentPoint = allData[nums[j]][i];
if (j == )
{
lastValue = currentValue;
lastPoint = currentPoint;
}
if (currentValue != lastValue)
{
double shang1 = CalEntropy(count1, all1);
double shang2 = CalEntropy(count2, all2);
double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2);
allShang = (-totalShang + allShang);
if (lianxuMax < allShang)
{
lianxuMax = allShang;
for (int k = ; k < count1.Length; k++)
{
leftCount[k] = count1[k];
rightCount[k] = count2[k];
}
splitPoint = j;
splitValue = (currentPoint + lastPoint) / ;
}
}
all1++;
count1[Convert.ToInt32(currentValue) - ]++;
count2[Convert.ToInt32(currentValue) - ]--;
all2--;
lastValue = currentValue;
lastPoint = currentPoint;
}
double rate1 = Convert.ToDouble(leftCount[] + leftCount[]) / (leftCount[] + leftCount[] + rightCount[] + rightCount[]);
chushu = ;
if (rate1 > )
{
chushu = chushu + rate1 * Math.Log(rate1, );
}
double rate2 = Convert.ToDouble(rightCount[] + rightCount[]) / (leftCount[] + leftCount[] + rightCount[] + rightCount[]);
if (rate2 > )
{
chushu = chushu + rate2 * Math.Log(rate2, );
}
//lianxuMax = lianxuMax ;
//lianxuMax = lianxuMax;
if (lianxuMax > jubuMax)
{
//info.setSplitIndex(i);
info.splitIndex=(i);
//info.setFeatures(new List<String> { splitValue + "" });
info.features = (new List<String> { splitValue + "" });
//info.setType(1);
info.type=();
jubuMax = lianxuMax;
//info.setType(1);
List<int>[] allInt = new List<int>[];
allInt[] = new List<int>();
allInt[] = new List<int>();
for (int k = ; k < splitPoint; k++)
{
allInt[].Add(nums[k]);
}
for (int k = splitPoint; k < nums.Count; k++)
{
allInt[].Add(nums[k]);
}
info.temp=(allInt);
//info.setTemp(allInt);
double[][] alls = new double[][];
alls[] = new double[leftCount.Length];
alls[] = new double[leftCount.Length];
for (int k = ; k < leftCount.Length; k++)
{
alls[][k] = leftCount[k];
alls[][k] = rightCount[k];
}
info.class_Count=(alls);
//info.setclassCount(alls);
}
}
#endregion
}
#region 如果找不到最佳的分裂属性，则设为叶节点
if (info.splitIndex == -)
{
double[] finalCount = node.ClassCount;
double max = finalCount[];
int result = ;
for (int i = ; i < finalCount.Length; i++)
{
if (finalCount[i] > max)
{
max = finalCount[i];
result = (i + );
}
}
node.feature_Type=("result");
node.features=(new List<String> { "" + result });
return node;
}
#endregion
#region 分裂
int deep = node.deep;
node.SplitFeature=("" + info.splitIndex); List<Node> childNode = new List<Node>();
int[] used = new int[isUsed.Length];
for (int i = ; i < used.Length; i++)
{
used[i] = isUsed[i];
}
if (info.type == )
{
used[info.splitIndex] = ;
node.feature_Type=("离散");
}
else
{
used[info.splitIndex] = ;
node.feature_Type=("连续");
}
int sumLeaf = ;
int sumWrong = ;
List<int>[] rowIndex = info.temp;
List<String> features = info.features;
for (int j = ; j < rowIndex.Length; j++)
{
if (rowIndex[j].Count == )
{
continue;
}
if (info.type == )
features.Add("" + (j + ));
Node node1 = new Node();
node1.setClassCount(info.class_Count[j]);
node1.deep=(deep + );
node1.rowCount = info.temp[j].Count;
node1 = findBestSplit(node1, info.temp[j], used);
sumLeaf += node1.leafNode_Count;
sumWrong += node1.leafWrong;
childNode.Add(node1);
}
node.leafNode_Count = (sumLeaf);
node.leafWrong = (sumWrong);
node.features=(features);
node.childNodes=(childNode);
#endregion
return node;
}
catch (Exception e)
{
Console.WriteLine(e.StackTrace);
return node;
}
}
（4）剪枝
悲观剪枝方法（PEP）：
public static void prune(Node node)
{
if (node.feature_Type == "result")
return;
double treeWrong = node.getErrorCount() + 0.5;
double leafError = node.leafWrong + 0.5 * node.leafNode_Count;
double var = Math.Sqrt(leafError * ( - Convert.ToDouble(leafError) / node.nums.Count));
double panbie = leafError + var - treeWrong;
if (panbie > )
{
node.feature_Type=("result");
node.childNodes=(null);
int result = (node.result + );
node.features=(new List<String>() { "" + result });
}
else
{
List<Node> childNodes = node.childNodes;
for (int i = ; i < childNodes.Count; i++)
{
prune(childNodes[i]);
}
}
}
C4.5核心算法的所有源代码：
#region C4.5核心算法
/// <summary>
/// 测试
/// </summary>
/// <param name="node"></param>
/// <param name="data"></param>
public static String findResult(Node node, String[] data)
{
List<String> featrues = node.features;
String type = node.feature_Type;
if (type == "result")
{
return featrues[];
}
int split = Convert.ToInt32(node.SplitFeature);
List<Node> childNodes = node.childNodes;
double[] resultCount = node.ClassCount;
if (type == "连续")
{
double value = Convert.ToDouble(featrues[]);
if (Convert.ToDouble(data[split]) <= value)
{
return findResult(childNodes[], data);
}
else
{
return findResult(childNodes[], data);
}
}
else
{
for (int i = ; i < featrues.Count; i++)
{
if (data[split] == featrues[i])
{
return findResult(childNodes[i], data);
}
if (i == featrues.Count - )
{
double count = resultCount[];
int maxInt = ;
for (int j = ; j < resultCount.Length; j++)
{
if (count < resultCount[j])
{
count = resultCount[j];
maxInt = j;
}
}
return findResult(childNodes[], data);
}
}
}
return null;
}
/// <summary>
/// 判断是否还需要分裂
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
public static bool ifEnd(Node node, double entropy,int[] isUsed)
{
try
{
double[] count = node.ClassCount;
int rowCount = node.rowCount;
int maxResult = ;
#region 数达到某一深度
int deep = node.deep;
if (deep >= maxDeep)
{
maxResult = node.result + ;
node.feature_Type=("result");
node.features=(new List<String>() { maxResult + "" });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 纯度(其实跟后面的有点重了，记得要修改)
//maxResult = 1;
//for (int i = 1; i < count.Length; i++)
//{
// if (count[i] / rowCount >= 0.95)
// {
// node.feature_Type=("result");
// node.features=(new List<String> { "" + (i + 1) });
// node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1]));
// node.leafNode_Count = 1;
// return true;
// }
//}
#endregion
#region 熵为0
if (entropy == )
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { maxResult + "" });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 属性已经分完
bool flag = true;
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
flag = false;
break;
}
}
if (flag)
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
#region 数据量少于100
if (rowCount < Limit_Node)
{
maxResult = node.result+;
node.feature_Type=("result");
node.features=(new List<String> { "" + (maxResult) });
node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - ]));
node.leafNode_Count = ;
return true;
}
#endregion
return false;
}
catch (Exception e)
{
return false;
}
}
#region 排序算法
public static void InsertSort(double[] values, List<int> arr, int StartIndex, int endIndex)
{
for (int i = StartIndex + ; i <= endIndex; i++)
{
int key = arr[i];
double init = values[i];
int j = i - ;
while (j >= StartIndex && values[j] > init)
{
arr[j + ] = arr[j];
values[j + ] = values[j];
j--;
}
arr[j + ] = key;
values[j + ] = init;
}
}
static int SelectPivotMedianOfThree(double[] values, List<int> arr, int low, int high)
{
int mid = low + ((high - low) >> );//计算数组中间的元素的下标 //使用三数取中法选择枢轴
if (values[mid] > values[high])//目标: arr[mid] <= arr[high]
{
swap(values, arr, mid, high);
}
if (values[low] > values[high])//目标: arr[low] <= arr[high]
{
swap(values, arr, low, high);
}
if (values[mid] > values[low]) //目标: arr[low] >= arr[mid]
{
swap(values, arr, mid, low);
}
//此时，arr[mid] <= arr[low] <= arr[high]
return low;
//low的位置上保存这三个位置中间的值
//分割时可以直接使用low位置的元素作为枢轴，而不用改变分割函数了
}
static void swap(double[] values, List<int> arr, int t1, int t2)
{
double temp = values[t1];
values[t1] = values[t2];
values[t2] = temp;
int key = arr[t1];
arr[t1] = arr[t2];
arr[t2] = key;
}
static void QSort(double[] values, List<int> arr, int low, int high)
{
int first = low;
int last = high; int left = low;
int right = high; int leftLen = ;
int rightLen = ; if (high - low + < )
{
InsertSort(values, arr, low, high);
return;
} //一次分割
int key = SelectPivotMedianOfThree(values, arr, low, high);//使用三数取中法选择枢轴
double inti = values[key];
int currentKey = arr[key]; while (low < high)
{
while (high > low && values[high] >= inti)
{
if (values[high] == inti)//处理相等元素
{
swap(values, arr, right, high);
right--;
rightLen++;
}
high--;
}
arr[low] = arr[high];
values[low] = values[high];
while (high > low && values[low] <= inti)
{
if (values[low] == inti)
{
swap(values, arr, left, low);
left++;
leftLen++;
}
low++;
}
arr[high] = arr[low];
values[high] = values[low];
}
arr[low] = currentKey;
values[low] = values[key];
//一次快排结束
//把与枢轴key相同的元素移到枢轴最终位置周围
int i = low - ;
int j = first;
while (j < left && values[i] != inti)
{
swap(values, arr, i, j);
i--;
j++;
}
i = low + ;
j = last;
while (j > right && values[i] != inti)
{
swap(values, arr, i, j);
i++;
j--;
}
QSort(values, arr, first, low - - leftLen);
QSort(values, arr, low + + rightLen, last);
}
#endregion
/// <summary>
/// 寻找最佳的分裂点
/// </summary>
/// <param name="num"></param>
/// <param name="node"></param>
public static Node findBestSplit(Node node, List<int> nums, int[] isUsed)
{
try
{
//判断是否继续分裂
double totalShang = CalEntropy(node.ClassCount, node.rowCount);
if (ifEnd(node, totalShang,isUsed))
{
return node;
}
#region 变量声明
SplitInfo info = new SplitInfo();
int RowCount = nums.Count; //样本总数
double jubuMax = ; //局部最大熵
#endregion
for (int i = ; i < isUsed.Length - ; i++)
{
if (isUsed[i] == )
{
continue;
}
#region 离散变量
if (type[i] == )
{
int[] allFeatureCount = new int[]; //所有类别的数量
double[][] allCount = new double[allNum[i]][];
for (int j = ; j < allCount.Length; j++)
{
allCount[j] = new double[classCount];
}
int[] countAllFeature = new int[allNum[i]];
List<int>[] temp = new List<int>[allNum[i]];
for (int j = ; j < temp.Length; j++)
{
temp[j] = new List<int>();
}
for (int j = ; j < nums.Count; j++)
{
int index = Convert.ToInt32(allData[nums[j]][i]);
temp[index - ].Add(nums[j]);
countAllFeature[index - ]++;
allCount[index - ][Convert.ToInt32(allData[nums[j]][lieshu - ]) - ]++;
}
double allShang = ;
double chushu = ;
for (int j = ; j < allCount.Length; j++)
{
allShang = allShang + CalEntropy(allCount[j], countAllFeature[j]) * countAllFeature[j] / RowCount;
if (countAllFeature[j] > )
{
double rate = countAllFeature[j] / Convert.ToDouble(RowCount);
chushu = chushu + rate * Math.Log(rate, );
}
}
allShang = (-totalShang + allShang);
if (allShang > jubuMax)
{
info.features = new List<string>();
info.type = ;
info.temp = temp;
info.splitIndex = i;
info.class_Count = allCount;
jubuMax = allShang;
allFeatureCount = countAllFeature;
}
}
#endregion
#region 连续变量
else
{
double[] leftCount = new double[classCount]; //做节点各个类别的数量
double[] rightCount = new double[classCount]; //右节点各个类别的数量
double[] count1 = new double[classCount]; //子集1的统计量
//double[] count2 = new double[node.getCount().Length]; //子集2的统计量
double[] count2 = new double[node.ClassCount.Length]; //子集2的统计量
for (int j = ; j < node.ClassCount.Length; j++)
{
count2[j] = node.ClassCount[j];
}
int all1 = ; //子集1的样本量
int all2 = nums.Count; //子集2的样本量
double lastValue = ; //上一个记录的类别
double currentValue = ; //当前类别
double lastPoint = ; //上一个点的值
double currentPoint = ; //当前点的值
int splitPoint = ;
double splitValue = ;
double[] values = new double[nums.Count];
for (int j = ; j < values.Length; j++)
{
values[j] = allData[nums[j]][i];
}
QSort(values, nums, , nums.Count - );
double chushu = ;
double lianxuMax = ; //连续型属性的最大熵
for (int j = ; j < nums.Count - ; j++)
{
currentValue = allData[nums[j]][lieshu - ];
currentPoint = allData[nums[j]][i];
if (j == )
{
lastValue = currentValue;
lastPoint = currentPoint;
}
if (currentValue != lastValue)
{
double shang1 = CalEntropy(count1, all1);
double shang2 = CalEntropy(count2, all2);
double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2);
allShang = (-totalShang + allShang);
if (lianxuMax < allShang)
{
lianxuMax = allShang;
for (int k = ; k < count1.Length; k++)
{
leftCount[k] = count1[k];
rightCount[k] = count2[k];
}
splitPoint = j;
splitValue = (currentPoint + lastPoint) / ;
}
}
all1++;
count1[Convert.ToInt32(currentValue) - ]++;
count2[Convert.ToInt32(currentValue) - ]--;
all2--;
lastValue = currentValue;
lastPoint = currentPoint;
}
double rate1 = Convert.ToDouble(leftCount[] + leftCount[]) / (leftCount[] + leftCount[] + rightCount[] + rightCount[]);
chushu = ;
if (rate1 > )
{
chushu = chushu + rate1 * Math.Log(rate1, );
}
double rate2 = Convert.ToDouble(rightCount[] + rightCount[]) / (leftCount[] + leftCount[] + rightCount[] + rightCount[]);
if (rate2 > )
{
chushu = chushu + rate2 * Math.Log(rate2, );
}
//lianxuMax = lianxuMax ;
//lianxuMax = lianxuMax;
if (lianxuMax > jubuMax)
{
//info.setSplitIndex(i);
info.splitIndex=(i);
//info.setFeatures(new List<String> { splitValue + "" });
info.features = (new List<String> { splitValue + "" });
//info.setType(1);
info.type=();
jubuMax = lianxuMax;
//info.setType(1);
List<int>[] allInt = new List<int>[];
allInt[] = new List<int>();
allInt[] = new List<int>();
for (int k = ; k < splitPoint; k++)
{
allInt[].Add(nums[k]);
}
for (int k = splitPoint; k < nums.Count; k++)
{
allInt[].Add(nums[k]);
}
info.temp=(allInt);
//info.setTemp(allInt);
double[][] alls = new double[][];
alls[] = new double[leftCount.Length];
alls[] = new double[leftCount.Length];
for (int k = ; k < leftCount.Length; k++)
{
alls[][k] = leftCount[k];
alls[][k] = rightCount[k];
}
info.class_Count=(alls);
//info.setclassCount(alls);
}
}
#endregion
}
#region 如果找不到最佳的分裂属性，则设为叶节点
if (info.splitIndex == -)
{
double[] finalCount = node.ClassCount;
double max = finalCount[];
int result = ;
for (int i = ; i < finalCount.Length; i++)
{
if (finalCount[i] > max)
{
max = finalCount[i];
result = (i + );
}
}
node.feature_Type=("result");
node.features=(new List<String> { "" + result });
return node;
}
#endregion
#region 分裂
int deep = node.deep;
node.SplitFeature=("" + info.splitIndex); List<Node> childNode = new List<Node>();
int[] used = new int[isUsed.Length];
for (int i = ; i < used.Length; i++)
{
used[i] = isUsed[i];
}
if (info.type == )
{
used[info.splitIndex] = ;
node.feature_Type=("离散");
}
else
{
used[info.splitIndex] = ;
node.feature_Type=("连续");
}
int sumLeaf = ;
int sumWrong = ;
List<int>[] rowIndex = info.temp;
List<String> features = info.features;
for (int j = ; j < rowIndex.Length; j++)
{
if (rowIndex[j].Count == )
{
continue;
}
if (info.type == )
features.Add("" + (j + ));
Node node1 = new Node();
node1.setClassCount(info.class_Count[j]);
node1.deep=(deep + );
node1.rowCount = info.temp[j].Count;
node1 = findBestSplit(node1, info.temp[j], used);
sumLeaf += node1.leafNode_Count;
sumWrong += node1.leafWrong;
childNode.Add(node1);
}
node.leafNode_Count = (sumLeaf);
node.leafWrong = (sumWrong);
node.features=(features);
node.childNodes=(childNode);
#endregion
return node;
}
catch (Exception e)
{
Console.WriteLine(e.StackTrace);
return node;
}
}
/// <summary>
/// 计算熵
/// </summary>
/// <param name="counts"></param>
/// <param name="countAll"></param>
/// <returns></returns>
public static double CalEntropy(double[] counts, int countAll)
{
try
{
double allShang = ;
for (int i = ; i < counts.Length; i++)
{
if (counts[i] == )
{
continue;
}
double rate = counts[i] / countAll;
allShang = allShang + rate * Math.Log(rate, );
}
return allShang;
}
catch (Exception e)
{
return ;
}
} #region 悲观剪枝
public static void prune(Node node)
{
if (node.feature_Type == "result")
return;
double treeWrong = node.getErrorCount() + 0.5;
double leafError = node.leafWrong + 0.5 * node.leafNode_Count;
double var = Math.Sqrt(leafError * ( - Convert.ToDouble(leafError) / node.rowCount));
double panbie = leafError + var - treeWrong;
if (panbie > )
{
node.feature_Type = "result";
node.childNodes = null;
int result = node.result + ;
node.features= new List<String>() { "" + result };
}
else
{
List<Node> childNodes = node.childNodes;
for (int i = ; i < childNodes.Count; i++)
{
prune(childNodes[i]);
}
}
}
#endregion
#endregion
总结：
要记住，C4.5是分类树最终要的算法，算法的思想其实很简单，但是分类的准确性高。可以说C4.5是ID3的升级版和强化版，解决了ID3未能解决的问题。要重点记住以下几个方面：
1.C4.5是采用信息增益率选择分裂的属性，解决了ID3选择属性时的偏向性问题；
2.C4.5能够对连续数据进行处理，采用一刀切的方式将连续型的数据切成两份，在选择切割点的时候使用信息增益作为择优的条件；
3.C4.5采用悲观剪枝的策略，一定程度上降低了过拟合的影响。
决策树系列（四）——C4.5的更多相关文章
- 大白话5分钟带你走进人工智能-第二十六节决策树系列之Cart回归树及其参数(5)
第二十六节决策树系列之Cart回归树及其参数(5) 上一节我们讲了不同的决策树对应的计算纯度的计算方法, ...
- 前端构建大法 Gulp 系列 (四)：gulp实战
前端构建大法 Gulp 系列 (一):为什么需要前端构建 前端构建大法 Gulp 系列 (二):为什么选择gulp 前端构建大法 Gulp 系列 (三):gulp的4个API 让你成为gulp专家 前 ...
- Netty4.x中文教程系列(四) 对象传输
Netty4.x中文教程系列(四) 对象传输 我们在使用netty的过程中肯定会遇到传输对象的情况,Netty4通过ObjectEncoder和ObjectDecoder来支持. 首先我们定义一个U ...
- S5PV210开发系列四_uCGUI的移植
S5PV210开发系列四 uCGUI的移植 象棋小子 1048272975 GUI(图形用户界面)极大地方便了非专业用户的使用,用户无需记忆大量的命令,取而代之的是能够通过窗体.菜单 ...
- WCF编程系列(四)配置文件
WCF编程系列(四)配置文件 .NET应用程序的配置文件 前述示例中Host项目中的App.config以及Client项目中的App.config称为应用程序配置文件,通过该文件配置可控制程序的 ...
- SQL Server 2008空间数据应用系列四：基础空间对象与函数应用
原文:SQL Server 2008空间数据应用系列四:基础空间对象与函数应用 友情提示,您阅读本篇博文的先决条件如下: 1.本文示例基于Microsoft SQL Server 2008 R2调测. ...
- VSTO之旅系列(四)：创建Word解决方案
原文:VSTO之旅系列(四):创建Word解决方案 本专题概要 引言 Word对象模型 创建Word外接程序 小结 一.引言 在上一个专题中主要为大家介绍如何自定义我们的Excel 界面的,然而在这个 ...
- 系列四TortoiseSvn客户端软件
原文:系列四TortoiseSvn客户端软件 TortoiseSvn介绍 TortoiseSvn 是 Subversion 版本控制系统的一个免费开源客户端,可以超越时间的管理文件和目录.文件保存在中 ...
- 【C++自我精讲】基础系列四 static
[C++自我精讲]基础系列四 static 0 前言 变量的存储类型:存储类型按变量的生存期划分,分动态存储方式和静态存储方式. 1)动态存储方式的变量,生存期为变量所在的作用域.即程序运行到此变量时 ...
- java基础解析系列(四)---LinkedHashMap的原理及LRU算法的实现
java基础解析系列(四)---LinkedHashMap的原理及LRU算法的实现 java基础解析系列(一)---String.StringBuffer.StringBuilder java基础解析 ...
随机推荐
- ASCII Art (English)
Conmajia, 2012 Updated on Feb. 18, 2018 What is ASCII art? It's graphic symbols formed by ASCII char ...
- 自动创建字符设备，不需mknod
自动创建设备文件 1.自动创建设备文件的流程 字符设备驱动模块 -->创建一个设备驱动class--->创建属于class的device--->调用mdev工具(自动完成)--> ...
- virtualbox命令行共享CentOS目录
virtualbox命令行共享CentOS目录 1. 安装virtualbox增强工具 "右ctrl+c" 显示和隐藏virtualbox虚拟机的菜单栏. 在VirtualBo ...
- table内容强制换行
为防止文字过长而撑坏表格,一般我们需要通过css使td中内容强制换行.分别给table和td加一条样式即可实现: <meta charset="utf-8"> < ...
- H-ui.admin v2.3后台模版！
一个很好的 后台开发模板 演示地址 http://demo.h-ui.net/H-ui.admin/3.1/index.html 下载地址 http://downs.h-ui.net/h-ui/H-u ...
- PHP中的浮点精度和类型
PHP中的浮点数 精度 在PHP中,浮点数的字长和平台相关,通常最大值是 1.8e308 并具有 14 位十进制数字的精度(64 位 IEEE 格式). 浮点数的精度有限.尽管取决于系统,PHP 通常 ...
- python进阶学习笔记（二）
1.模块和包的概念 python的解决方案是把同名的模块放到不同的包中 1.1,导入模块 要使用一个模块,我们必须首先导入该模块.Python使用import语句导入一个模块.例如,导入系统自带的模块 ...
- Java经典编程题50道之十
一球从100米高度自由落下,每次落地后反跳回原高度的一半:再落下……求它在第10次落地时,共经过多少米?第10次反弹多高? public class Example10 { public sta ...
- NoSQL性能测试工具YCSB-Running a Workload
写在前面 目前,在系统设计中引入了越来越多的NoSQL产品,例如Redis/ MongoDB/ HBase等,其中性能指标往往会成为权衡不同NoSQL产品的关键因素.对这些产品在性能表现和产品选择上的 ...
- Java反射获取字节码以及判断类型
一.获取类的字节码的三种方法: 1.使用Class.class Class<?> c1=String.class; 2.使用实例.getClass() String s= Clas ...