洛谷P4609 [FJOI2016]建筑师 【第一类斯特林数】

题目链接

洛谷P4609

题解

感性理解一下：



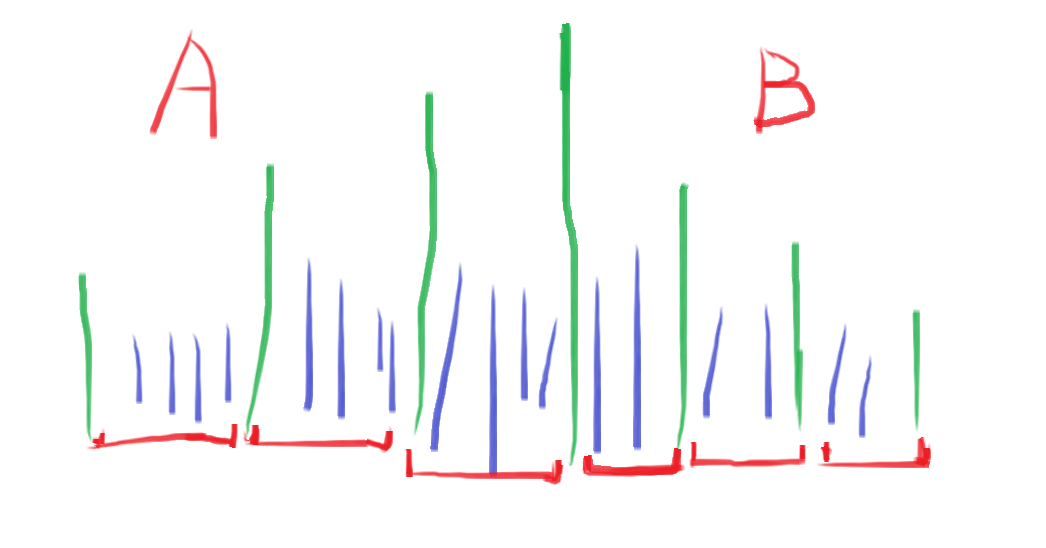
一神带\(n\)坑

所以我们只需将除了\(n\)外的\(n - 1\)个元素分成\(A + B - 2\)个集合，每个集合选出最大的在一端，剩余进行排列，然后选出\(A - 1\)个集合放左边，剩余放右边

容易发现分割集合并内部排列实质对应第一类斯特林数$$\begin{bmatrix} n - 1 \ A + B - 2 \end{bmatrix}$$

所以答案就是

\[\begin{bmatrix} n - 1 \\ A + B - 2 \end{bmatrix} {A + B - 2 \choose A - 1}
\]

\(O(n(A + B) + (A + B))\)预处理第一类斯特林数和组合数即可

递推式

\[\begin{bmatrix} n \\ m \end{bmatrix} = \begin{bmatrix} n - 1 \\ m - 1 \end{bmatrix} + \begin{bmatrix} n - 1 \\ m \end{bmatrix}(n - 1)
\]

真不知道这题是怎么打到深蓝的

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 50005,maxm = 205,INF = 1000000000,P = 1000000007;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int s[maxn][maxm],N = 50000,M = 200;
int fac[maxm],fv[maxm];
inline int qpow(int a,int b){
	int re = 1;
	for (; b; b >>= 1,a = 1ll * a * a % P)
		if (b & 1) re = 1ll * re * a % P;
	return re;
}
void init(){
	fac[0] = 1;
	for (int i = 1; i < maxm; i++) fac[i] = 1ll * fac[i - 1] * i % P;
	fv[maxm - 1] = qpow(fac[maxm - 1],P - 2); fv[0] = 1;
	for (int i = maxm - 2; i; i--) fv[i] = 1ll * fv[i + 1] * (i + 1) % P;
	s[0][0] = 1;
	for (int i = 1; i <= N; i++){
		int E = min(i,M);
		for (int j = 1; j <= E; j++)
			s[i][j] = (s[i - 1][j - 1] + 1ll * s[i - 1][j] * (i - 1) % P) % P;
	}
}
inline int C(int n,int m){
	return 1ll * fac[n] * fv[m] % P * fv[n - m] % P;
}
int main(){
	init();
	int T = read(),n,A,B;
	while (T--){
		n = read(); A = read(); B = read();
		printf("%lld\n",1ll * s[n - 1][A + B - 2] * C(A + B - 2,A - 1) % P);
	}
	return 0;
}