【[LNOI2014]LCA】

这题好神啊

能够\(1A\)真是不可思议

首先看到要求的这个柿子\(\sum_{i=l}^{r}deep[LCA(i,z)]\)，而且\(l\)和\(r\)并不是来自与一棵子树或者一条链，而是编号连续的一段

所以肯定没有什么办法可以一下子求出来这么多的\(LCA\)的

得想个好的办法转化一下

于是就想往主席树上想

首先\(z\)的\(lca\)肯定是在\(z\)到根的路径上的，于是我们可以定住\(lca\)，来求这个\(lca\)对答案的贡献

于是我们有一个主席树的暴力

我们就枚举\(z\)到根的路径上的点，对于这些每一个点，我们求出在其子树内部有多少个大于\(l\)小于\(r\)的点，乘上深度,这就是这个\(lca\)的贡献

吗？

显然不是，我们得减去那些在下面的那些子树里就已经算过了的数

所以我们会暴力啦，真开心

那我们想一下如何优化暴力

先来看看答案长什么样子

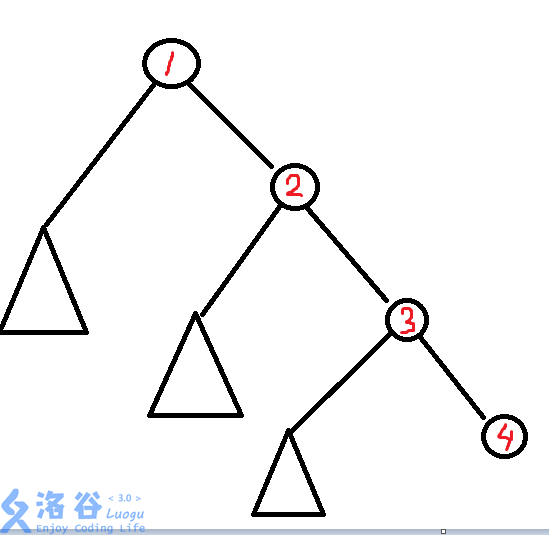
好吧，我画的还是很难看，这可是魏佬钦定

我们设\(sum_i\)表示在\(i\)的子树内部有多少个符合条件的点

于是我们的答案可以写成

\[4*sum_4+3*(sum_3-sum_4)+2*(sum_2-sum_3)+1*(sum_1-sum_2)
\]

之后就会惊奇的发现答案竟然就是\(sum_4+sum_3+sum_2+sum_1\)

那我们怎么维护啊，难道要硬上主席树？

显然不用啊

既然没有强制在线，我们就离线+树剖呗

一个点显然只会对他本身到根上这条路径的点产生贡献，于是就是一个树剖板子了

同时查询也是一个简单的根路径查询

至于如何统计答案，我们将询问排序，之后可以将插入顺序想象成时间轴，于是就可以差分求解了

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define re register
#define maxn 50005
const int mod=201314;
struct E
{
	int v,nxt;
}e[maxn<<1];
struct Ask
{
	int x,y,z,rk;
}a[maxn];
int n,m,num,Q,cnt;
int top[maxn],deep[maxn],fa[maxn],to[maxn],sum[maxn],son[maxn],head[maxn];
int l[maxn<<2],r[maxn<<2],tag[maxn<<2],d[maxn<<2];
int Lans[maxn],Rans[maxn];
inline void add_edge(int x,int y)
{
	e[++num].v=y;
	e[num].nxt=head[x];
	head[x]=num;
}
inline int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9')
		x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x;
}
void build(int x,int y,int i)
{
	l[i]=x,r[i]=y,d[i]=0,tag[i]=0;
	if(x==y) return;
	int mid=x+y>>1;
	build(x,mid,i<<1),build(mid+1,y,i<<1|1);
}
inline void pushdown(int i)
{
	if(!tag[i]) return;
	tag[i<<1]+=tag[i];
	if(tag[i<<1]>mod) tag[i<<1]%=mod;
	tag[i<<1|1]+=tag[i];
	if(tag[i<<1|1]>mod) tag[i<<1|1]%=mod;
	d[i<<1]+=(r[i<<1]-l[i<<1]+1)*tag[i];
	d[i<<1]%=mod;
	d[i<<1|1]+=(r[i<<1|1]-l[i<<1|1]+1)*tag[i];
	d[i<<1|1]%=mod;
	tag[i]=0;
}
void change(int x,int y,int i)
{
	if(x<=l[i]&&y>=r[i])
	{
		tag[i]++;
		d[i]+=r[i]-l[i]+1;
		if(d[i]>mod) d[i]%=mod;
		return;
	}
	pushdown(i);
	int mid=l[i]+r[i]>>1;
	if(y<=mid) change(x,y,i<<1);
		else if(x>mid) change(x,y,i<<1|1);
			else change(x,y,i<<1),change(x,y,i<<1|1);
	d[i]=(d[i<<1]+d[i<<1|1])%mod;
}
int query(int x,int y,int i)
{
	if(x<=l[i]&&y>=r[i]) return d[i];
	pushdown(i);
	int mid=l[i]+r[i]>>1;
	if(y<=mid) return query(x,y,i<<1);
	if(x>mid) return query(x,y,i<<1|1);
	return (query(x,y,i<<1)+query(x,y,i<<1|1))%mod;
}
void dfs1(int x)
{
	sum[x]=1;
	int maxx=-1;
	for(re int i=head[x];i;i=e[i].nxt)
	if(!deep[e[i].v])
	{
		deep[e[i].v]=deep[x]+1;
		fa[e[i].v]=x;
		dfs1(e[i].v);
		sum[x]+=sum[e[i].v];
		if(sum[e[i].v]>maxx) maxx=sum[e[i].v],son[x]=e[i].v;
	}
}
void dfs2(int x,int topf)
{
	top[x]=topf;
	to[x]=++cnt;
	if(!son[x]) return;
	dfs2(son[x],topf);
	for(re int i=head[x];i;i=e[i].nxt)
	if(deep[e[i].v]>deep[x]&&son[x]!=e[i].v) dfs2(e[i].v,e[i].v);
}
inline void tree_change(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(deep[top[x]]<deep[top[y]]) std::swap(x,y);
		change(to[top[x]],to[x],1);
		x=fa[top[x]];
	}
	if(deep[x]>deep[y]) std::swap(x,y);
	change(to[x],to[y],1);
}
inline int tree_query(int x,int y)
{
	int ans=0;
	while(top[x]!=top[y])
	{
		if(deep[top[x]]<deep[top[y]]) std::swap(x,y);
		ans+=query(to[top[x]],to[x],1);
		if(ans>mod) ans%=mod;
		x=fa[top[x]];
	}
	if(deep[x]>deep[y]) std::swap(x,y);
	ans+=query(to[x],to[y],1);
	return ans%mod;
}
inline int cmp(Ask K,Ask M)
{
	return K.x<M.x;
}
inline int cop(Ask K,Ask M)
{
	return K.y<M.y;
}
int main()
{
	n=read(),Q=read();
	int Fa;
	for(re int i=1;i<n;i++)
		Fa=read(),add_edge(Fa,i);
	deep[0]=1;
	dfs1(0);
	dfs2(0,0);
	build(1,n,1);
	for(re int i=1;i<=Q;i++)
		a[i].x=read(),a[i].y=read(),a[i].z=read(),a[i].rk=i;
	std::sort(a+1,a+Q+1,cmp);
	int tot=1;
	for(re int i=-1;i<n;i++)
	{
		if(i>=0) tree_change(i,0);
		while(a[tot].x-1==i)
		{
			Lans[a[tot].rk]=tree_query(a[tot].z,0);
			tot++;
		}
	}
	build(1,n,1);
	std::sort(a+1,a+Q+1,cop);
	tot=1;
	for(re int i=0;i<n;i++)
	{
		tree_change(i,0);
		while(a[tot].y==i)
		{
			Rans[a[tot].rk]=tree_query(a[tot].z,0);
			tot++;
		}
	}
	for(re int i=1;i<=Q;i++)
	printf("%d\n",(Rans[i]-Lans[i]+mod)%mod);
	return 0;
}