数论——算数基本定理 - HDU 4497 GCD and LCM

GCD and LCM

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 3379    Accepted Submission(s): 1482

Problem Description

Given two positive integers G and L, could you tell me how many solutions of (x, y, z) there are, satisfying that gcd(x, y, z) = G and lcm(x, y, z) = L? 
Note, gcd(x, y, z) means the greatest common divisor of x, y and z, while lcm(x, y, z) means the least common multiple of x, y and z. 
Note 2, (1, 2, 3) and (1, 3, 2) are two different solutions.

 

Input

First line comes an integer T (T <= 12), telling the number of test cases. 
The next T lines, each contains two positive 32-bit signed integers, G and L. 
It’s guaranteed that each answer will fit in a 32-bit signed integer.

 

Output

For each test case, print one line with the number of solutions satisfying the conditions above.

 

Sample Input

2
6 72
7 33

 

Sample Output

72
0

---

gcd(x,y,z) == G， lcm(x,y,z) == L

x' = x /G,y' = y /G ，z' = z / G; 　　gcd( x', y',z') == 1,lcm(x',y',z') == L/G

这样的话对t = L/G 这个数进行素因子分解，t = p1^t1 * p2^t2 * p3^t3 ..... * pn ^tn;

满足上面条件的x,y,z一定为这样的形式。
x' = p1^i1 * p2^i2 *```* pn^in.
y' = p1^j1 * p2^j2 * ```*pn^jn.
z' = p1^k1 * p2^k2 * ```*pn^kn.
为了满足上面的条件，对于p1,一定有max(i1,j1,k1) = t1和min(i1,j1,k1) =0；

因为gcd（p1^i1,p1^j1,p1^k1）== 1  → min(i1,j1,k1) == 0；lcm(p1^i1,p1^j1,p1^k1) == p1^t1   => max(i1,j1,k1) == t1;

所以我们现在要做的是把L/G分解成n个素因数相乘，比如：28=2*2*7=2^2 * 7

对于每一个p来说，三个数的集合一定是{ 0, t, x | 0≤x≤t }

1. x = 0 或 x = t：这种情况有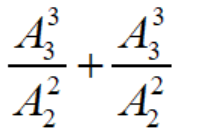= 6 种
2. 0 < x < t：这种情况x的取值可以为 0~t 的整数，一共有 t-1 个，而每一个数，都可以有种排列方法，就是6*(t-1)

   所以对每一个P来说，最后一共有 6*t 种取法 。

举个例子：252=2*2*7=2^2 * 3^3 * 7 一共有6*2+6*3+6=36种不同的（x，y，z）序列。

而如果L%G!=0，自然就没有解

#include <iostream>
using namespace std;

int f1(int n) {
    , i = ;
    ) {
        ;
        ){
        ) {
            t++;
            n /= i;
        }
            res *=  * t;
        }
            i++;
    }
    return res;
}
int main() {
    int T;
    cin >> T;
    while (T--) {
        int G, L;
        cin >> G >> L;
        )
            cout <<  << endl;
        else
            cout << f1(L / G) << endl;
    }
    ;
}