【BZOJ2440】[中山市选2011]完全平方数

题意描述

　原题

　　

　一句话描述：

　　求第K个不是完全平方数的倍数的数。

　　K≤$10^{9}$

------------------------------------------

题解：

　　首先，直接求第$k$个不是完全平方数倍数的数不好求，我们不妨将它转换为一个判定问题：对于一个确定的常数$x$,他是不是第k个不是完全平方数倍数的数。这句话等价于：$[1,x]$是否有k个不是完全平方数倍数的数，这个怎么求呢？

　　根据容斥原理，答案就是：0个质数乘积的平方的倍数的数量（1的倍数）- 1个质数乘积的平方的倍数的数量（4,9,25的倍数）+ 2个质数乘积的平方的倍数的数量（36,100的倍数）。

　　恰好发现，$i^2$对应的符号就是$μ(i)$,所以答案就是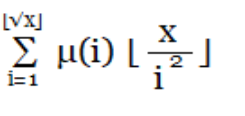

　　　那么我们二分一下$x$,就能找到答案了。二分的范围是$[1,k*2]$.

　　代码实现：

　　

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
const int maxn = 1e6+;
typedef long long ll;
int mu[maxn],prime[maxn],vis[maxn];
void init_mu(int n){
    int cnt=;
    mu[]=;
    for(int i=;i<n;i++){
        if(!vis[i]){
            prime[cnt++]=i;
            mu[i]=-;
        }
        for(int j=;j<cnt&&i*prime[j]<n;j++){
            vis[i*prime[j]]=;
            if(i%prime[j]==)   {mu[i*prime[j]]=;break;}
            else { mu[i*prime[j]]=-mu[i];}
        }
    }
}
inline ll find(ll x) {
    ll least = sqrt(x+0.5),ans=;
    for(register int i=;i<=least;i++) {
        ans+=mu[i]*x/(1LL*i*i);
    }
    return ans;
}
inline ll calc(ll k) {
    ll l = ,r = k<<;
    while(l<r) {
        ll mid = (r+l)>>;
        ll temp = find(mid);
#ifdef DEBUG
        printf("%d %d %d\n",l,r,temp);
#endif
        if(temp<k) l=mid+;
        else r=mid;
    }
    return r;
}
int T;
ll k;
int main() {
    init_mu();
    scanf("%d",&T);
    while(T--) {
        scanf("%lld",&k);
        printf("%lld\n",calc(k));
    }
    return ;
}