HDU-1423 最长公共上升子序列（LCIS）

问题描述:###

给定两个字符串x, y, 求它们公共子序列s, 满足si < sj ( 0 <= i < j < |s|).要求S的长度是所有条件序列中长度最长的.

做过最长公共子序列应该更容易明白了。

定义状态d[i][j]表示以a数组的前i个元素，b数组的前j个元素并且以b[j]为结尾的LCIS的长度。

首先：a[i] ！= b[j]时， d[i][j] = d[i-1][j]; 因为 d[i][j] 是以 b[j] 为结尾的LCIS，如果 d[i][j] > 0 那么就说明 a[1] .... a[i] 中必然有一个元素 a[k] 等于 b[j]。因为 a[k] != a[i]，那么 a[i] 对 d[i][j] 没有贡献，于是我们不考虑它照样能得出 d[i][j] 的最优值。所以在 a[i] != b[j] 的情况下必然有 d[i][j] = d[i-1][j]。这一点参考LCS的处理方法。

当a[i]==b[j]时， 首先，这个等于起码保证了长度为1的LCIS。然后我们还需要去找一个最长的且能让b[j]接在其末尾的LCIS。之前最长的LCIS在哪呢？首先我们要去找的d数组的第一维必然是i-1。因为i已经拿去和b[j]配对去了，不能用了。第二维需要枚举 b[1] ... b[j-1]了，因为你不知道这里面哪个最长且哪个小于 b[j]。

状态转移方程：###

a[i] != b[j]: d[i][j]=d[i-1][j] ；

a[i] == b[j]: d[i][j]=max(d[i-1][k]) + 1 ； （1<= k <= j-1）

不难看到，这是一个时间复杂度为O(n^3)的DP，离平方还有一段距离。

但是，这个算法最关键的是，如果按照一个合理的递推顺序，max(d[i-1][k])的值我们可以在之前访问 d[i][k] 的时候通过维护更新一个max变量得到。怎么得到呢？首先递推的顺序必须是状态的第一维在外层循环，第二维在内层循环。也就是算好了 d[1][n2] 再去算 d[2][1]。 如果按照这个递推顺序我们可以在每次外层循环的开始加上令一个max变量为0，然后开始内层循环。当a[i]>b[j]的时候令max = d[i-1][j]。如果循环到了a[i] == b[j]的时候，则令 d[i][j] = max+1。 最后答案是 d[n1][1] ... d[n1][n2]的最大值。

举个例子

a={1， 4， 2， 5， -12} b ={5, -12, 1, 2, 4, 5}

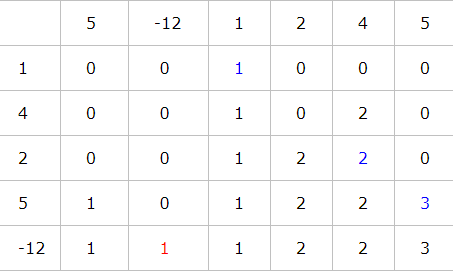
 if(a[i] == b[j])
    d[i][j] = mx + 1;
 else  if(a[i] > b[j] && mx < d[i-1][j])
            mx = d[i-1][j];
 //只有当a[i] > b[j]时，才更新mx， 保证了所求序列是上升的。

仔细看表格会发现： 若d[i][j] > 0 的话，那么在数组a前i个元素中一定存在a[k]( 1 <= k <= i)等于b[j]. 否则说明前i个a元素中没有与b[j]相同的元素。

//O(n^3) DP 实现

#include<bits/stdc++.h>
using namespace std;
int m1,m2,a[505],b[505],maxx,top=1,flag;
int f[505][505];

int main()
{
	cin>>m1;
	for(int i=1;i<=m1;i++)
		cin>>a[i];
	cin>>m2;
	for(int j=1;j<=m2;j++)
		cin>>b[j];

	for(int i=1;i<=m1;i++)
	{
		for(int j=1;j<=m2;j++)
		{
			f[i][j]=f[i-1][j];
			if(a[i]==b[j])
			{
				int Max=0;
				for(int k=1;k<=j-1;k++)
					if(b[j]>b[k])
						Max=max(Max,f[i-1][k]);
				f[i][j]=Max+1;
			}
		}
	}
	cout<<f[m1][m2]<<endl;
	maxx=f[m1][m2];
	for(int i=1;i<=m1;i++)
	{
		for(int j=1;j<=m2;j++)
		{
			if(f[i][j]==top)
			{
				cout<<a[i]<<" ";
				flag=1;
				break;
			}
		}
		if(flag==1)
		{
			top++;  flag=0;
		}
		if(top>maxx)
			break;
	}
	return 0;
}

//O(n^2) DP 实现

#include<iostream>
#include<cstdio>
#include<string.h>
#include<cstring>
#include<math.h>
using namespace std;

int n1, n2, t, k;
int a[505], b[505], d[505][505];
int dp()
{
    int mx;
    for(int i = 1; i <= n1; i++)
    {
        mx = 0;
        for(int j = 1; j <= n2; j++)
        {
            d[i][j] = d[i-1][j];
            if(a[i] > b[j] && mx < d[i-1][j]) mx = d[i-1][j];
            else if(a[i] == b[j])
                d[i][j] = mx + 1;
        }
    }
    mx = 0;
    for(int i = 1; i <= n2; i++)
    {
        if(d[n1][i] > mx)
             mx = d[n1][i];
    }
    return mx;
}
int main()
{
    cin >> t;
    while(t--)
    {
        scanf("%d", &n1);
        for(int i = 1; i <= n1; i++) scanf("%d", &a[i]);
        scanf("%d", &n2);
        for(int i = 1; i <= n2; i++) scanf("%d", &b[i]);
        memset(d, 0, sizeof(d));
        int ans = dp();
        printf("%d\n", ans);
        if(t) printf("\n");
    }
    return 0;
}