【算法】单源最短路——Dijkstra

对于固定起点的最短路算法，我们称之为单源最短路算法。单源最短路算法很多，最常见的就是dijkstra算法。

dijkstra主要用的是一种贪心的思想，就是说如果i...s...t...j是最短路，那么i和j之间的任意两点s,t之间也一定是最短路，非常好证，如果s，t之间不是最短路，那么必然存在最短路，那么i到j也不是最短路造成了矛盾。

而dijkstra就是运用这样的思想，把起点首先放进一个集合S中，其他的点在另一个集合中，每次取起点经过集合S中的点可达的最短路的点，加入到集合S中，并且根据新加入的店刷新一遍最短路。直到所有的点都在集合S中。

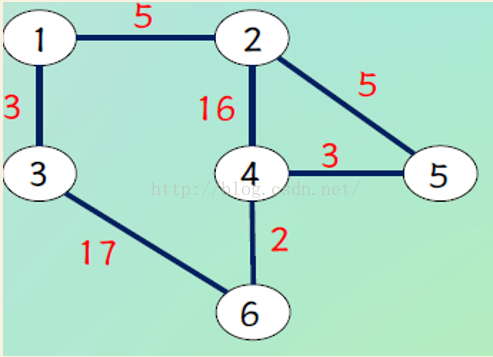
如上图，假设以1为起点，dis[i]为起点到i点的最短距离，如果没法直达则为INF

第一次：S中只有1，那么1能直达的点有2，3，取路径最短的3加入S，并更新一遍dis，发现6可达，dis[6] = 20；

第二次：S中有1，3，可达的有2，6，取2，则4，5可达，dis[4] = 21,dis[5] = 10；

第三次：S中有1，2，3，可达的有4，5，6，取5，到4多了新路径且比原来近，更新dis[4] = 13；

第四次：S中有1，2，3，5，可达的有4，6，取4，到6多了新路径且比原来近，更新dis[6] = 15；

第五次：S中有1，2，3，4，5，可达的有6，只有6不在S中，取6，不更新，完成算法

要注意的是外围循环是除了起点外的点数，如果多一次，pos会无法赋值因为所有的点都遍历过了，造成变量没有初始化而程序崩溃。

代码如下：

1. #include <cstdio>
2. #include <algorithm>
3. #include <cstring>
4. using namespace std;
5. const int maxn = 10;
6. int map[maxn][maxn], dis[maxn];
7. int n;                                                         //点数
8. void init()
9. {
10. for (int i = 1; i <= n; i++)
11. for (int j = 1; j <= n; j++)
12. map[i][j] = 0x3f3f3f;
13. memset(dis, 0, sizeof(dis));
14. }
15. void dijkstra(int v0)
16. {
17. for (int i = 1; i <= n; i++)
18. dis[i] = map[v0][i];
19. map[v0][v0] = 0;
20. for (int i = 1; i < n; i++)                                //注意循环的次数，如果到n，最后一次所有的map[i][i]都是0，pos找不到值会崩溃，如果初始化为0则dis[i]最后全是0（dis[0] = 0）
21. {
22. int min_dis = 0x3f3f3f3f,pos;
23. for (int j =1; j <= n; j++)
24. {
25. if (map[j][j] && dis[j] < min_dis)                 //遍历所有点找到距离v0最小的点，记录下距离，并将其加入已计算的集合，将其编号用pos记录下来
26. min_dis = dis[pos = j];
27. }
28. map[pos][pos] = 0;                                     //用map[i][i]来表示某个点是否被访问过，节省空间
29. for (int j = 1; j <= n; j++)
30. {
31. dis[j] = min(dis[j], dis[pos] + map[pos][j]);      //用新添加的点来更新一边dis
32. }
33. }
34. }
35. int main()
36. {
37. freopen("input.txt", "r", stdin);
38. int m,u,v,w,target;
39. scanf("%d%d", &n,&m);
40. init();
41. while (m--)
42. {
43. scanf("%d%d%d", &u, &v, &w);
44. map[u][v] = map[v][u] = w;
45. }
46. scanf("%d", &target);
47. dijkstra(target);
48. for (int i = 1; i <= n; i++)
49. {
50. printf("%d : %d\n", i, dis[i]);
51. }
52. return 0;
53. }

但要注意的是，dijkstra不能计算含有负权的图的最短路，因为一直加负数始终会比原来的小。