2019-oo-第一单元总结

第一单元总结

——表达式的求导

一、思路综述

二、代码分析

　　结构分析

　　bug分析

　　风格分析

三、Hack Hack Hack

四、难点总结

五、感想

一、思路综述

第一次作业

输入处理时，一项一项地用正则表达式进行匹配（本来用大正则，结果爆栈QwQ），其中第一项要单独考虑。创建Polynomial（多项式）和Term（项）两个类，Polynomial类中用HashMap保存项，一边添加项一边合并。注意到正项放在第一个要比负项放在第一个的结果短。

第二次作业

仍然用正则表达式的方式处理输入表达式。构建了Expression（表达式）、Term（项），Factor（因子）三类，另外构建了三元组的Struct类，用来存放x因子、sin因子、cos因子的指数。在表达式类中，仍然用HashMap的方式存放项，求导方法调用项类的求导方法。在项类中，以“*”为分隔符分割成多个因子，遍历每一个因子，构造Facotr实例，通过kind属性给相应的因子种类指数加一。

需要注意的是，在三元组的结构体内，要重写方法hashCode和equals，才能继续正确使用HashMap的containsKey和put方法来合并同类项。

对于化简表达式，想秃了也没有找到全面的合并方法，最后考虑了sin(x)^2+cos(x)^2=1，cos(x)^a*sin(x)^4-cos(x)^a*sin(x)^2=sin(x)^2*-cos(x)^a+2，sin(x)^a*cos(x)^4-sin(x)^a*cos(x)^2=cos(x)^2*-sin(x)^a+2三种化简方式。

血的教训是优化前请一定先考虑正确性！！！

public int hashCode() {
            int result = 17;
            result = result * 37 + this.xindex.hashCode();
            result = result * 37 + this.sinindex.hashCode();
            result = result * 37 + this.cosindex.hashCode();
            return result;
}

 public boolean equals(Object another) {
            return (this.getXindex().compareTo(
                    ((Expression.Struct) another).getXindex()) == 0
                    && this.getSinindex().compareTo(
                    ((Expression.Struct) another).getSinindex()) == 0
                    && this.getCosindex().compareTo(
                    ((Expression.Struct) another).getCosindex()) == 0);
}

第三次作业

第三次作业进行了很多次重构，起初考虑用正则表达式一项一项地进行匹配，边判断合法性边加入到项的arraylist中。其中嵌套因子的正则表达式被写为"((sin)|(cos))[ \\t]*\\(.+\\)[ \\t]*"，然而形如sin(x)+cos(x)的表达式也会被匹配成功，在后续嵌套因子的求导中被判为WF。

因此最后先判断合法性（通过不断匹配"[ \\t]*\\(" + expression + "\\)[ \\t]*"，其中expression为第二次作业中的合法表达式，并将其替换为x，直到最后的表达式成为第二次作业中的合法表达式，若不能，则不合法。）；

再进行项的匹配，用stack的自增自减来模拟括号的进栈，遇到“（”，stack++，遇到“）”，stack--，当且仅当遇到“+”，“-”时stack==0，且“+-”前不为“*”和“^”时，“+”“-”才能作为加减运算符来对待，也就是说这个时候才是一项的结束；

类似地，在每一项中，要进行因子的匹配，当且仅当遇到“*”时stack==0，才表示一个因子的结束，在项类中用arraylist存放每一个因子；

SinFactor，CosFactor，CoefFactor，ExpFactor，NestFactor类均继承自Factor类，在Facor类中，判断其属于哪一个子类，同时进一步判断其合法性。

以上的所有类都有同一个接口Exprsision，在这个接口中，有共享的正则表达式，和diff方法。每一个Factor子类均有自己的求导方法，Factor类的求导方法是根据它的type属性调用其子类的求导方法。Term类的求导方法即乘积项的求导，ExpFactor的求导方法即加和项的求导，求导方法直接返回字符串。

写得太惨了qwq，根本没能考虑优化。

二、代码分析

2.1结构分析

注：

ev(G)：即Essentail Complexity，用来表示一个方法的结构化程度

iv(G)：即Design Complexity，用来表示一个方法和他所调用的其他方法的紧密程度，值越大联系越紧密。

v(G)：即循环复杂度，可以理解为穷尽程序流程每一条路径所需要的试验次数。

OCavg：类的方法的平均循环复杂度。

WMC：类的方法的总循环复杂度。

第一次作业

仅包含poly和term两级。

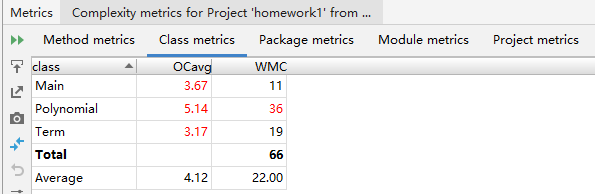
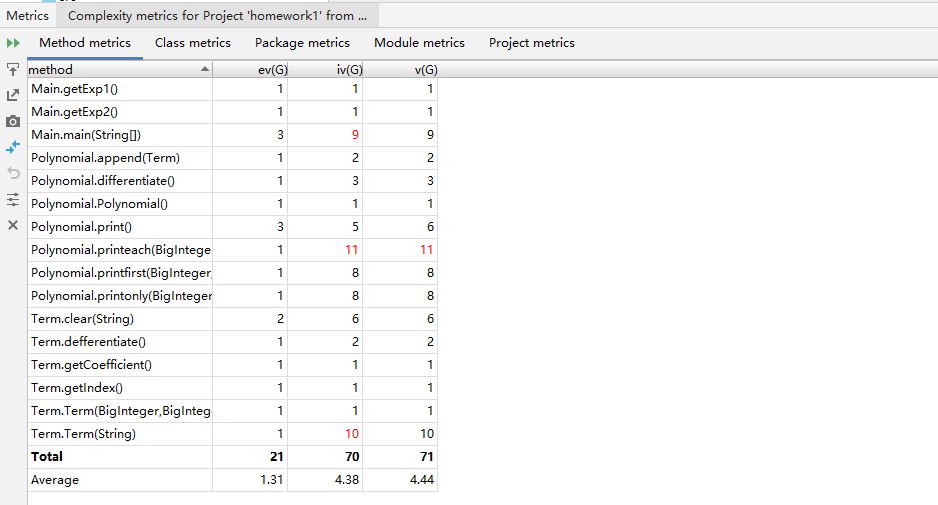
在Polynomial类的print方法中，分别考虑了，只有一个项——printonly，第一个项——printeach，其他的项——printeach，可以看出来printeach的iv和循环复杂度都很高。

第二次作业

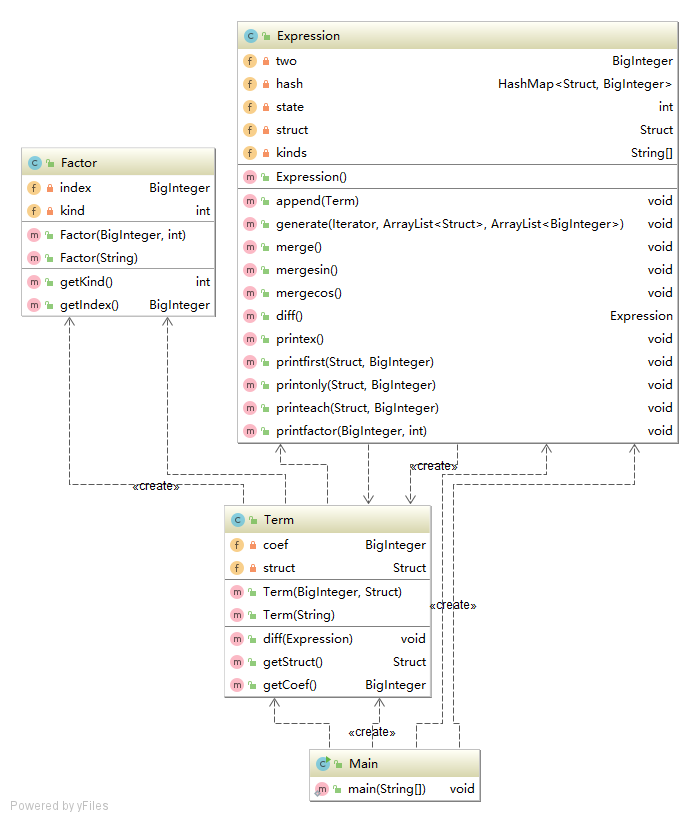
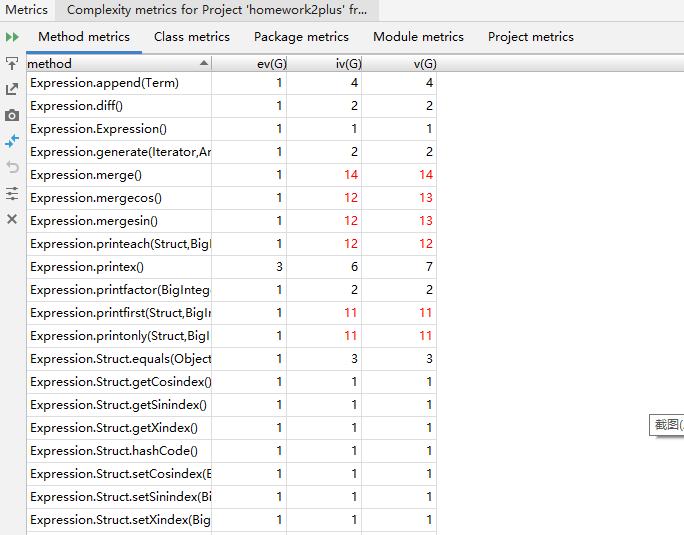
三级结构，即Expression-Term-Factor，其中Factor类的复杂度偏低，Expression和Term类复杂度偏高，其中，Expression类的打印和合并同类项的相关方法的iv和循环复杂度明显高于其他方法。

第三次作业

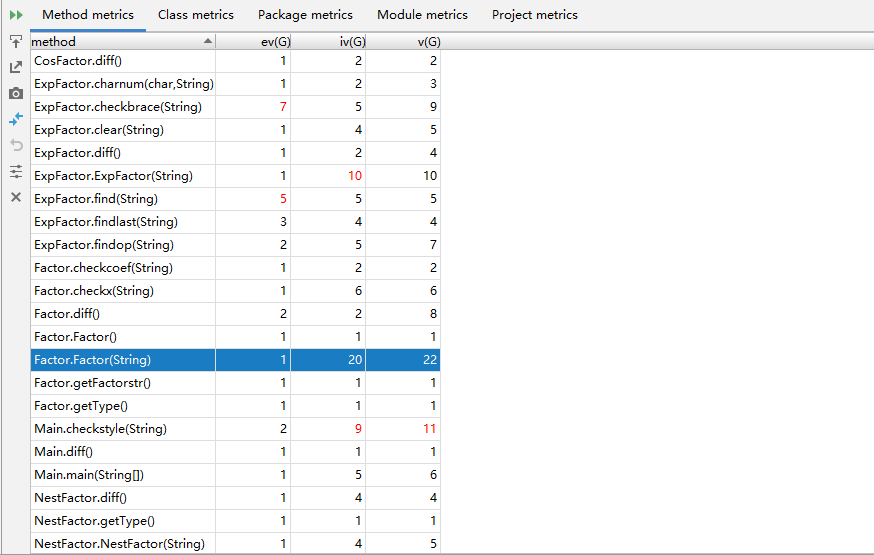
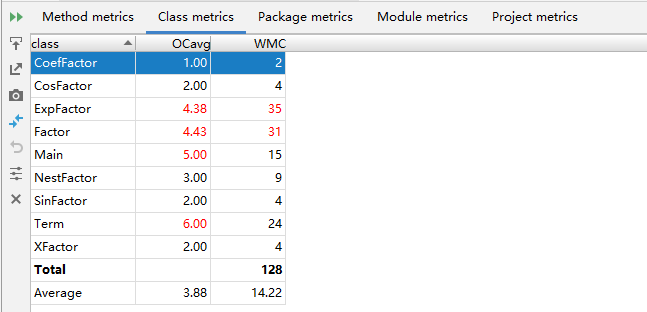
同样可以认为这是三级结构，Exp-Term-Factor，区别只是Exp也有可能为因子。

当Main方法处理完输入字符串的正确性后，若不是表达式因子，就在两侧加上括号，变成表达式因子。ExpFactor类的构造方法中，将传入的字符串分割成两个arraylist，分别用来存放项，以及项与项之间的符号。而Term类中又包含了存放Factor的arraylist，其中的Factor也有可能是ExpFactor类， 所有类都有接口Expression。ExpFactor，SinFactor，CosFactor，CoefFactor和XFactor继承自Factor类。

2.2Bug分析

第一次作业

容易出bug的地方有：大正则爆栈，\s匹配空白符忽略了\v,\f，结果只有一个0时没有输出。

然而只考虑了输出为1项，答案为0的情况，未考虑结果的几项均为0，即0*x^2+0*x^5+0*x^3这样的情况，挨了一刀，还是来自友军的误伤（发出嘤嘤嘤的菜叫）！

第二次作业

好像是在处理项与项连接有三个正负号的时候出现了问题，具体情况记不清了，上oo网站发现bug修复关闭了，看不见了（挠头.gif）。想了好久的优化，结果强测挂了两个点……正确性才是王道！

第三次作业

出现了一些粗心的小bug，很幸运地被强测放过，很惨地被互测刀死了。小bug的问题来源都是忘了考虑空格，比如下面这个情况，当系数或指数中有空格时，可能把正确的项判为WF。

public void checkcoef(String str) {
        try {
            BigInteger big = new BigInteger(str.trim());
        } catch (NumberFormatException e) {
            System.out.println("WRONG FORMAT!\n");
            System.exit(0);
        }
}

2.3风格分析

·正则表达式的部分，采用分级的形式会使代码显得更简洁明了，如：

String factor = "(([+-]?\\d+)|" +
                "(((sin[ \\t]*\\([ \\t]*x[ \\t]*\\)[ \\t]*)|" +
                "(cos[ \\t]*\\([ \\t]*x[ \\t]*\\)[ \\t]*)|x)[ \\t]*" +
                "(\\^[ \\t]*[+-]?\\d+)?))";
String term = "((([+-]?[ \\t]*" + factor +
                "[ \\t]*)|([+-][ \\t]*[+-]\\d+))[ \\t]*"
                + "(\\*[ \\t]*" + factor + "[ \\t]*)*)";
String expression = "^[ \\t]*[+-]?[ \\t]*" + term
                + "([ \\t]*[+-][ \\t]*" + term + "[ \\t]*)*$";

·养成了优化代码风格的意识，从全靠Ctrl+Alt+l和checkstyle，到有意识地把代码写得美观一些，控制方法的长度等等。

三、Hack hack hack

首先是拿自己和小伙伴的样例一顿盲狙，这些样例基本上是针对我们觉得自己处理得比较麻烦的地方，比如说第一次的爆栈，结果是0的输出（要命的是我拿这个hack到了别人，结果自己也有问题）。盲狙的过程中，有的时候简短的数据更容易测到bug。

第一次作业的盲狙过后，构造了自认为覆盖性比较好的测试数据，之后的两次样例太复杂了，就省略了这一步。

在此之外，有的时候会看一下具体代码，比如第一次作业，有同学没有考虑表达式结尾部分的正确性；第二次作业，有同学在正则表达式中直接写了"\\d{1,4}"，只要超过四位的整数就会出bug；这样有针对性地de一会，也有较大几率能看出问题。然而看别人的代码有的时候是真读不懂，不过第一次互测时，在一段怎么也读不懂作者意图的代码中找到了bug。

四、难点总结

WF

前两次比较容易用正则表达式进行匹配，第三次由于嵌套因子和表达式因子的存在，很难直接判断一个表达式的合法性，故考虑先判断整体结构的合法性，再局部地对每一个项、因子进行合法性的判断，具体实现在前文中有所描述。

项/因子的提取

前两次都是用正则表达式直接一项一项的匹配，在第三次作业中，要对括号进行进出栈处理，栈为空才有可能是一个项或者一个因子的结束，否则是嵌套因子或表达式因子的内部。

优化

第一次和第二次都用HashMap来存储项，第一次的key是指数index，第二次的key是一个三元组的类，表示sin项、cos项、x项的指数。第一次要注意把正项提前，第二次要围绕sin（x）^2+cos（x）^2=1做文章。第三次作业中，由于diff方法的返回值直接是字符串，不方便进行优化，而且为了保险起见，该加括号的地方都加了，0和1也不敢太省，总的来说就得到了一个非常丑陋的求导结果。

实际上，可以考虑做一些简单的优化：

1、输入处理过程中，对由简单因子构成的嵌套因子或表达式因子，进行如作业一、二的合并同类项。比如：sin((x^2+3*x^2+x))可以化简为sin((4*x^2+x))。再进行求导。

2、为每一个因子的求导结果保存一个系数属性，在项的求导中，把系数相乘合并起来。当一个项的系数为0时，后面的因子可以不做考虑。

3、进行括号匹配，当两层括号中没有其他内容时，可以消去一层括号，比如：将cos((((((x))))))化简成cos(x)。

五、感想（Applying Creational Pattern）

三次作业整体的结构（即Expression-Term-Factor）没有变化，但每一次都重构了很多部分。

在第一次作业中没有建立求导方法的层层调用，直接在poly类中进行了求导，在第二次作业中熟悉了HashMap的hashCode、equals方法，更明显地感受到三个类之间的层次关系，在Poly类的求导方法中调用了Term类的求导方法。第三次作业中，进行了大量的重构，包括表达式合法性的判断，抽象出了一个checkstyle方法；设计了Expression接口，清晰了diff方法，也使很多正则表达式得以在几个类之间共享；设计了多个因子的子类，继承Factor类；ExpFactor类和Term类的相互调用；递归性地求导等等。

总的教训是，一定要先把架构想清楚，再写代码，第三次作业反复重构的很大一部分原因都来自于没有考虑清楚层与层之间的关系，子类和父类之间的关系，某一个方法到底是该交给父类还是交给子类，等等。