*42. Trapping Rain Water 接雨水

1. 原始题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

2. 思路

最简单的想法：对于每个元素都要考虑它能接多少雨水：

第一个元素是0，能接0雨水

第二个元素是1，能接0雨水

第三个元素是0，能接1雨水

...

第六个元素是0，能接2雨水。

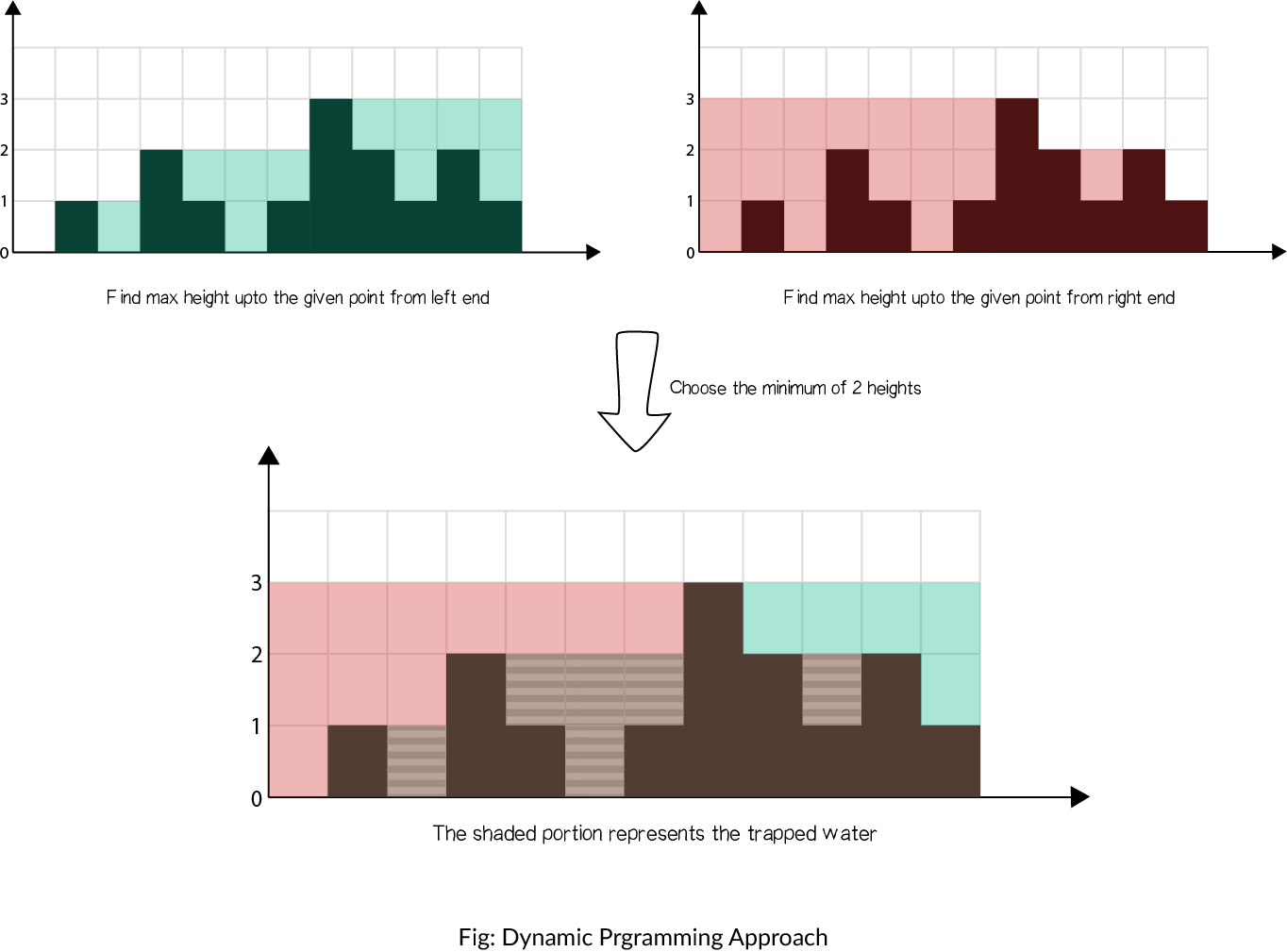
可以看到，每个元素能接的雨水量是：当前位置左边最高的数与右边最高的数的最小值减去当前位置的数。

例如第六个元素接水量为2 = min(2,3)-0=2。

总结：对于每个位置，都考虑其左边最高的墙和右边最高的墙即可。

3. 解题

思路图：

 class Solution:
     def trap(self, height):
         if not height: return 0
         n = len(height)
         left,right = [0]*n, [0]*n     # 每个位置都存放其左边最大值和右边最大值
         temp = 0
         for i in range(n):
             temp= max(temp,height[i]) # 找每个元素的左边最大值（含自身）
             left[i] = temp
         temp = 0
         for i in range(n-1,-1,-1):
             temp = max(temp,height[i]) # 找每个元素的右边最大值（含自身）
             right[i] = temp
         res = 0
         for i in range(n):
             res+=min(left[i],right[i])-height[i]   # 最小的高度值-自身
         return res

方法2. 双指针法

还是一个思路：当前位置需要左右两堵墙的最小值减去当前值。

左右两端各设定一个指针，初始两堵墙。如果左端小于右端，则以右端为墙，当前值等于左墙和右墙的最小值减去当前值。

 class Solution:
     def trap(self, height):
         if not height: return 0

         left, right = 0 , len(height)-1         # 左右指针
         area = 0
         leftwall, rightwall = 0,0               # 左墙和右墙
         while(left<right):
             if height[left]<height[right]:      # 右边高，则以右端为墙
                 if leftwall>height[left]:       # 如果左墙也比当前位置高的话
                     area+=min(leftwall,height[right])-height[left]       # 面积就是两墙最低者减去当前位置的高度
                 else:
                     leftwall = height[left]     # 否则更新左墙
                 left+=1
             else:
                 if rightwall>height[right]:
                     area+=min(rightwall,height[left])-height[right]
                 else:
                     rightwall = height[right]
                 right-=1
         return area