增强学习（五）----- 时间差分学习(Q learning, Sarsa learning)

接下来我们回顾一下动态规划算法(DP)和蒙特卡罗方法(MC)的特点，对于动态规划算法有如下特性：

• 需要环境模型，即状态转移概率\(P_{sa}\)
• 状态值函数的估计是自举的(bootstrapping)，即当前状态值函数的更新依赖于已知的其他状态值函数。

相对的，蒙特卡罗方法的特点则有：

• 可以从经验中学习不需要环境模型
• 状态值函数的估计是相互独立的
• 只能用于episode tasks

而我们希望的算法是这样的：

• 不需要环境模型
• 它不局限于episode task，可以用于连续的任务

本文介绍的时间差分学习(Temporal-Difference learning, TD learning)正是具备了上述特性的算法，它结合了DP和MC，并兼具两种算法的优点。

TD Learing思想

在介绍TD learning之前，我们先引入如下简单的蒙特卡罗算法，我们称为constant-\(\alpha\) MC，它的状态值函数更新公式如下：
\[ V(s_t) \leftarrow V(s_t) + \alpha[R_t - V(s_t)] \tag {1}\]
其中\(R_t\)是每个episode结束后获得的实际累积回报，\(\alpha\)是学习率，这个式子的直观的理解就是用实际累积回报\(R_t\)作为状态值函数\(V(s_t)\)的估计值。具体做法是对每个episode，考察实验中\(s_t\)的实际累积回报\(R_t\)和当前估计\(V(s_t)\)的偏差值，并用该偏差值乘以学习率来更新得到\(V(S_t)\)的新估值。

现在我们将公式修改如下，把\(R_t\)换成\(r_{t+1} + \gamma V(s_{t+1})\)，就得到了TD(0)的状态值函数更新公式：
\[V(s_t) \leftarrow V(s_t) + \alpha[r_{t+1} + \gamma V(s_{t+1}) - V(s_t)] \tag {2}\]

为什么修改成这种形式呢，我们回忆一下状态值函数的定义：
\[V^{\pi}(s)=E_{\pi}[r(s'|s,a)+\gamma V^{\pi}(s')] \tag {3}\]
容易发现这其实是根据(3)的形式，利用真实的立即回报\(r_{t+1}\)和下个状态的值函数\(V(s_{t+1})\)来更新\(V(s_t)\)，这种就方式就称为时间差分(temporal difference)。由于我们没有状态转移概率，所以要利用多次实验来得到期望状态值函数估值。类似MC方法，在足够多的实验后，状态值函数的估计是能够收敛于真实值的。

那么MC和TD(0)的更新公式的有何不同呢？我们举个例子，假设有以下8个episode, 其中A-0表示经过状态A后获得了回报0:

index	samples
episode 1	A-0, B-0
episode 2	B-1
episode 3	B-1
episode 4	B-1
episode 5	B-1
episode 6	B-1
episode 7	B-1
episode 8	B-0

首先我们使用constant-\(\alpha\) MC方法估计状态A的值函数，其结果是\(V(A)=0\)，这是因为状态A只在episode 1出现了一次，且其累计回报为0。

现在我们使用TD(0)的更新公式，简单起见取\(\lambda=1\)，我们可以得到\(V(A)=0.75\)。这个结果是如何计算的呢？ 首先，状态B的值函数是容易求得的，B作为终止状态，获得回报1的概率是75%，因此\(V(B)=0.75\)。接着从数据中我们可以得到状态A转移到状态B的概率是100%并且获得的回报为0。根据公式(2)可以得到\(V(A) \leftarrow V(A) + \alpha[0 + \lambda V(B) - V(A)]\)，可见在只有\(V(A)=\lambda V(B)=0.75\)的时候，式(2)收敛。对这个例子，可以作图表示：

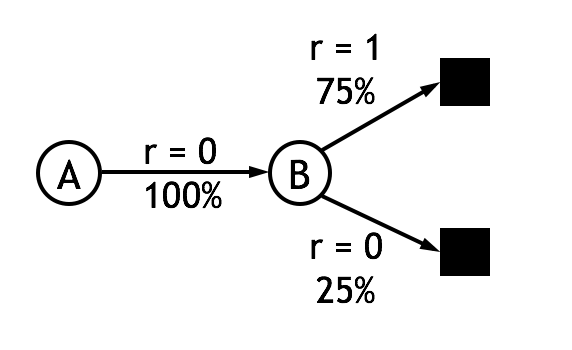
可见式(2)由于能够利用其它状态的估计值，其得到的结果更加合理，并且由于不需要等到任务结束就能更新估值，也就不再局限于episode task了。此外，实验表明TD(0)从收敛速度上也显著优于MC方法。

将式(2)作为状态值函数的估计公式后，前面文章中介绍的策略估计算法就变成了如下形式，这个算法称为TD prediction:

输入：待估计的策略\(\pi\)
任意初始化所有\(V(s)\)，(\(e.g.,V(s)=0,\forall s\in s^{+}\))
Repeat(对所有episode):
　　初始化状态 \(s\)
　　Repeat(对每步状态转移):
　　　　\(a\leftarrow\)策略\(\pi\)下状态\(s\)采取的动作
　　　　采取动作\(a\)，观察回报\(r\)，和下一个状态\(s'\)
　　　　\(V(s) \leftarrow V(s) + \alpha[r + \lambda V(s') - V(s)]\)
　　　　\(s\leftarrow s'\)
　　Until \(s_t\) is terminal
　Until 所有\(V(s)\)收敛
输出\(V^{\pi}(s)\)

Sarsa算法

现在我们利用TD prediction组成新的强化学习算法，用到决策/控制问题中。在这里，强化学习算法可以分为在策略(on-policy)和离策略(off-policy)两类。首先要介绍的sarsa算法属于on-policy算法。
与前面DP方法稍微有些区别的是，sarsa算法估计的是动作值函数(Q函数)而非状态值函数。也就是说，我们估计的是策略\(\pi\)下，任意状态\(s\)上所有可执行的动作a的动作值函数\(Q^{\pi}(s,a)\)，Q函数同样可以利用TD Prediction算法估计。如下就是一个状态-动作对序列的片段及相应的回报值。

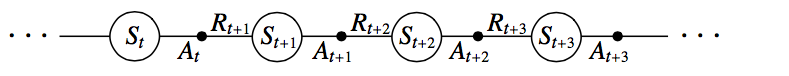
给出sarsa的动作值函数更新公式如下：
\[Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha[r_{t+1} + \lambda Q(s_{t+1}, a_{t+1}) - Q(s_t,a_t)] \tag {4}\]

可见式(4)与式(2)的形式基本一致。需要注意的是，对于每个非终止的状态\(s_t\)，在到达下个状态\(s_{t+1}\)后，都可以利用上述公式更新\(Q(s_t,A_t)\)，而如果\(s_t\)是终止状态，则要令\(Q(s_{t+1}=0,a_{t+1})\)。由于动作值函数的每次更新都与\((s_t, a_t,r_{t+1},s_{t+1},a_{t+1})\)相关，因此算法被命名为sarsa算法。sarsa算法的完整流程图如下：

算法最终得到所有状态-动作对的Q函数，并根据Q函数输出最优策略\(\pi\)

Q-learning

在sarsa算法中，选择动作时遵循的策略和更新动作值函数时遵循的策略是相同的，即\(\epsilon-greedy\)的策略，而在接下来介绍的Q-learning中，动作值函数更新则不同于选取动作时遵循的策略，这种方式称为离策略(Off-Policy)。Q-learning的动作值函数更新公式如下：
\[Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha[r_{t+1} + \lambda \max _{a} Q(s_{t+1}, a) - Q(s_t,a_t)] \tag {5}\]
可以看到，Q-learning与sarsa算法最大的不同在于更新Q值的时候，直接使用了最大的\(Q(s_{t+1},a)\)值——相当于采用了\(Q(s_{t+1},a)\)值最大的动作，并且与当前执行的策略，即选取动作\(a_t\)时采用的策略无关。 Off-Policy方式简化了证明算法分析和收敛性证明的难度，使得它的收敛性很早就得到了证明。Q-learning的完整流程图如下：

小结

本篇介绍了TD方法思想和TD(0),Q(0),Sarsa(0)算法。TD方法结合了蒙特卡罗方法和动态规划的优点，能够应用于无模型、持续进行的任务，并拥有优秀的性能，因而得到了很好的发展，其中Q-learning更是成为了强化学习中应用最广泛的方法。在下一篇中，我们将引入资格迹(Eligibility Traces)提高算法性能，结合Eligibility Traces后，我们可以得到\(Q(\lambda),Sarsa(\lambda)\)等算法

参考资料

[1] R.Sutton et al. Reinforcement learning: An introduction, 1998