4 多表代替密码之Hill 密码 2实现

该解密方法的KEY 不是一个数或者一段字符串，而是一个矩阵， 比如有个3*3的KEY：

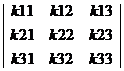
那么如果我们要加密一个长度为N的字符串， 那么把N除以3，分成M个3个字母组成的小段， 对每个小段尽心加密：

1. 将明文分成M个小段：{{p₁,p₂,p₃},{p₄,p₅,p₆}...{..p_N}}

2. 对每个小段尽心加密: c1 = (k11*p1 + k21*p2 + k31*p3)

　　　　　　　　　　　 c2= (k12*p1 + k22*p2 + k32*p3)

　　　　　　　　　　　c3= (k13*p1 + k23*p2 + k33*p3), 也就是：

密文C：[c1,c2,c3] = [p1,p2,p3] * KEY mod 26,

这样就可以得出Hill加密的算法是：

C = P*Kmod26；

那么对应的解密算法就是：

P = C * K^-1mod26.

下面是JAVA 实现：

package com.owner.replace.multi;

import Jama.Matrix;
import com.owner.util.matrix.MatrixUtil;

import java.text.NumberFormat;

/**
 * Created by wellmax on 2015/10/19.
 */
public class Hill {
    private final static Matrix KEY = new Matrix(new double[][]{{17,17,5},{21,18,21},{2,2,19}});
    private final static MatrixUtil MU = new MatrixUtil(KEY);
    private final static Matrix N_KEY = MU.inverse();
    private static int charToInt(char c){
        return (int)c - 97;
    }

    public String encrypt(String input){
        char[] chars = input.toCharArray();
        int[] numbers = new int[chars.length];
        for (int i = 0 ; i < chars.length ; i++){
            numbers[i] = charToInt(chars[i]);
        }
        int[] encrypts = MU.rowMultiplyMatrix(numbers,MU.getMatrix());
        for(int i = 0 ; i < encrypts.length ; i++){
            chars[i] = (char)(encrypts[i]+97);
        }
        return new String(chars);
    }
    public String decrypt(String input){
        char[] chars = input.toCharArray();
        int[] numbers = new int[chars.length];
        for (int i = 0 ; i < chars.length ; i++){
            numbers[i] = charToInt(chars[i]);
        }
        int[] decrypts = MU.rowMultiplyMatrix(numbers,N_KEY);
        for(int i = 0 ; i < decrypts.length ; i++){
            chars[i] = (char)(decrypts[i]+97);
        }
        return new String(chars);
    }

    public static void main(String[] args){
        Hill hill = new Hill();
        String encrypt = hill.encrypt("paymoremoney");
        System.out.println(encrypt);
        String decrypt = hill.decrypt(encrypt);
        System.out.println(decrypt);
    }
}

　对于3*3的KEY， 决定一个明文字母最后加密结果的因素：

1. 附近的2个字母；

2. KEY某一列的值

那么对于单个字母在密文中出现的频率来说是完全没有规律的， 同样的对于3*3的KEY， 双字母对出现的频率也是不定的。那么随着KEY维度的不断增大， 安全性就不断提高，因为不能通过字母或者字母对出现的频率来分析KEY的值。这对其他之前的加密来说无疑是质的提高。

但是这种加密仍是较易破解的， 典型的一个方法如下：

1. 不是所有的矩阵都有这种算法的逆矩阵， 这样KEY的取值范围就缩小了。

2. 可以通过验证步奏1中猜测的KEY是否正确， 我们通过猜测的KEY破解的密文可以用来判断KEY的正确性。

通过这两步就能较易的破解出KEY。

-Wellmaxwang