论文笔记:空间变换网络(Spatial Transformer Networks)
2015, NIPS
Max Jaderberg, Karen Simonyan, Andrew Zisserman, Koray Kavukcuoglu
Google DeepMind
为什么提出(Why)
- 一个理想中的模型:我们希望鲁棒的图像处理模型具有空间不变性,当目标发生某种转化后,模型依然能给出同样的正确的结果
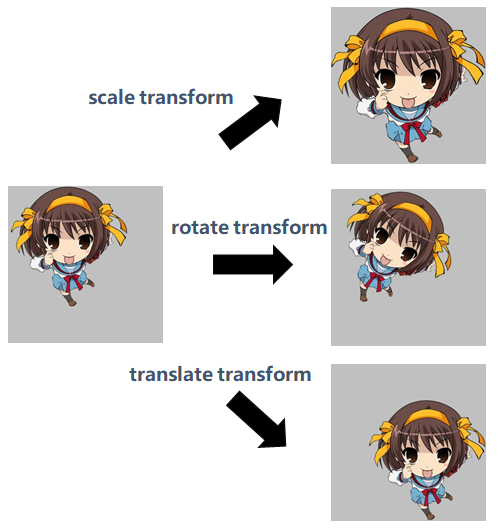
- 什么是空间不变性:举例来说,如下图所示,假设一个模型能准确把左图中的人物分类为凉宫春日,当这个目标做了放大、旋转、平移后,模型仍然能够正确分类,我们就说这个模型在这个任务上具有尺度不变性,旋转不变性,平移不变性
- CNN在这方面的能力是不足的:maxpooling的机制给了CNN一点点这样的能力,当目标在池化单元内任意变换的话,激活的值可能是相同的,这就带来了一点点的不变性。但是池化单元一般都很小(一般是2*2),只有在深层的时候特征被处理成很小的feature map的时候这种情况才会发生
- Spatial Transformer:本文提出的空间变换网络STN(Spatial Transformer Networks)可以使得模型具有空间不变性。
STN是什么(What)
- STN对feature map(包括输入图像)进行空间变换,输出一张新的图像。
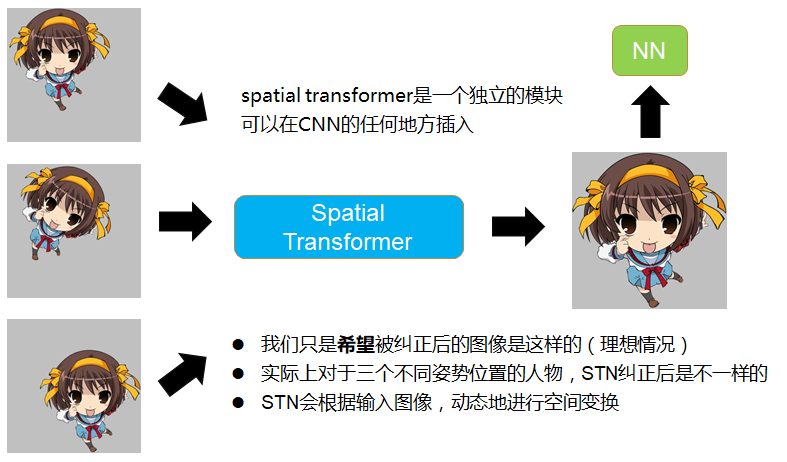
- 我们希望STN对feature map进行变换后能把图像纠正到成理想的图像,然后丢进NN去识别,举例来说,如下图所示,输入模型的图像可能是摆着各种姿势,摆在不同位置的凉宫春日,我们希望STN把它纠正到图像的正中央,放大,占满整个屏幕,然后再丢进CNN去识别。
- 这个网络可以作为单独的模块,可以在CNN的任何地方插入,所以STN的输入不止是输入图像,可以是CNN中间层的feature map
STN是怎么做的(How)
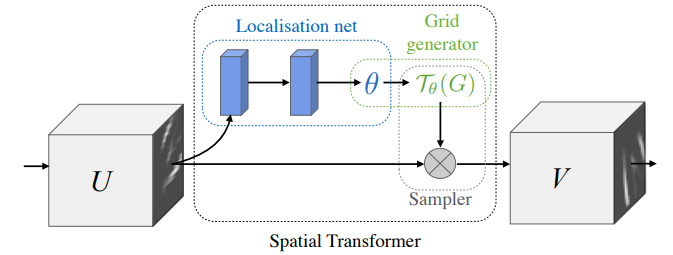
- 如下图所示,STN的输入为U,输出为V,因为输入可能是中间层的feature map,所以画成了立方体(多channel),STN主要分为下述三个步骤
- Localisation net:是一个自己定义的网络,它输入U,输出变化参数\(\Theta\),这个参数用来映射U和V的坐标关系
- Grid generator:根据V中的坐标点和变化参数\(\Theta\),计算出U中的坐标点。这里是因为V的大小是自己先定义好的,当然可以得到V的所有坐标点,而填充V中每个坐标点的像素值的时候,要从U中去取,所以根据V中每个坐标点和变化参数\(\Theta\)进行运算,得到一个坐标。在sampler中就是根据这个坐标去U中找到像素值,这样子来填充V
- Sampler:要做的是填充V,根据Grid generator得到的一系列坐标和原图U(因为像素值要从U中取)来填充,因为计算出来的坐标可能为小数,要用另外的方法来填充,比如双线性插值。
下面针对每个模块阐述一下
(1) Localisation net
这个模块就是输入U,输出一个变化参数\(\Theta\),那么这个\(\Theta\)具体是指什么呢?
我们知道线性代数里,图像的平移,旋转和缩放都可以用矩阵运算来做
举例来说,如果想放大图像中的目标,可以这么运算,把(x,y)中的像素值填充到(x',y')上去,比如把原来(2,2)上的像素点,填充到(4,4)上去。
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}2 &0\\0&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}0\\ 0\end{bmatrix}\)
如果想旋转图像中的目标,可以这么运算(可以在极坐标系中推出来,证明放到最后的附录)
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}cos \Theta & -sin \Theta\\ sin \Theta& cos\Theta\end{bmatrix} \begin{bmatrix}x\\ y\end{bmatrix}+\begin{bmatrix}0\\ 0\end{bmatrix}\)
这些都是属于仿射变换(affine transformation)
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}a & b \\ c& d\end{bmatrix} \begin{bmatrix}x\\ y\end{bmatrix}+\begin{bmatrix}e\\ f\end{bmatrix}\)
在仿射变化中,变化参数就是这6个变量,\(\Theta = \{a,b,c,d,e,f\}\)(此\(\Theta\)跟上述旋转变化里的角度\(\Theta\)无关)
这6个变量就是用来映射输入图和输出图之间的坐标点的关系的,我们在第二步grid generator就要根据这个变化参数,来获取原图的坐标点。
(2) Grid generator
有了第一步的变化参数,这一步是做个矩阵运算,这个运算是以目标图V的所有坐标点为自变量,以$ \Theta $为参数做一个矩阵运算,得到输入图U的坐标点。
\[ \begin{pmatrix}x_{i}^{s}\\ y_{i}^{s}\end{pmatrix}=\Theta \begin{pmatrix}x_{i}^{t}\\ y_{i}^{t}\\ 1\end{pmatrix}
=\begin{bmatrix}
\Theta _{11} & \Theta _{12} & \Theta _{13}\\ \Theta _{21}
& \Theta _{22} & \Theta _{23}
\end{bmatrix}\begin{pmatrix}
x_{i}^{t}\\ y_{i}^{t}
\\ 1
\end{pmatrix}\]
其中$ {(x_{i}^{t},y_{i}^{t})}$记为输出图V中的第i个坐标点,V中的长宽可以和U不一样,自己定义的,所以这里用i来标识第几个坐标点
$ {(x_{i}^{s},y_{i}^{s})}$记为输入图U中的点,这里的i是从V中对应过来的,表示V中的第i的坐标点映射的U中坐标,i跟U没有关系
(3) Sampler
由于在第二步计算出了V中每个点对应到U的坐标点,在这一步就可以直接根据V的坐标点取得对应到U中坐标点的像素值来进行填充,而不需要经过矩阵运算。需要注意的是,填充并不是直接填充,首先计算出来的坐标可能是小数,要处理一下,其次填充的时候往往要考虑周围的其它像素值。填充根据的公式如下。
\[V_{i}=\sum _n \sum _m U_{nm}*k(x_{i}^{s}-m;\phi _x)*k(y_{i}^{s}-n;\phi _y)\]
其中n和m会遍历原图U的所有坐标点,\(U_{nm}\)指原图U中某个点的像素值,k()为取样核,两个\(\phi\)为参数,\((x_{i}^{s},y_{i}^{s})\)表示V中第i个点要到U图中找的对应点的坐标,表示的坐标是U图上的,k表示使用不同的方法来填充,通常会使用双线性插值,则会得到下面的公式
\[V_{i}=\sum _n \sum _m U_{nm}*max(0, 1 - |x_{i}^{s}-m|)*max(0, 1 - |y_{i}^{s}-n|)\]
举例来说,我要填充目标图V中的(2,2)这个点的像素值,经过以下计算得到(1.6,2.4)
\[\begin{pmatrix}x_{i}^{s}\\ y_{i}^{s}\end{pmatrix}
=\begin{bmatrix}
\Theta _{11} & \Theta _{12} & \Theta _{13}\\ \Theta _{21}
& \Theta _{22} & \Theta _{23}
\end{bmatrix}\begin{pmatrix}
x_{i}^{t}\\ y_{i}^{t}
\\ 1
\end{pmatrix}\]
\[\begin{pmatrix}1.6\\ 2.4\end{pmatrix}
=\begin{bmatrix}
0 & 0.5 & 0.6\\ 1
& 0 & 0.4
\end{bmatrix}\begin{pmatrix}
2\\ 2
\\ 1
\end{pmatrix}\]
如果四舍五入后直接填充,则难以做梯度下降。
我们知道做梯度下降时,梯度的表现就是权重发生一点点变化的时候,输出的变化会如何。
如果用四舍五入后直接填充,那么(1.6,2.4)四舍五入后变成(2,2)
当\(\Theta\)(我们求导的时候是需要对\(\Theta\)求导的)有一点点变化的时候,(1.6,2.4)可能变成了(1.9,2.1)四舍五入后还是变成(2,2),输出并没有变化,对\(\Theta\)的梯度没有改变,这个时候没法用梯度下降来优化\(\Theta\)
如果采用上面双线性插值的公式来填充,在这个例子里就会考虑(2,2)周围的四个点来填充,这样子,当\(\Theta\)有一点点变化的时,式子的输出就会有变化,因为$(x_{i}^{s},y_{i}^{s}) $的变化会引起V的变化。注意下式中U的下标,第一个下标是纵坐标,第二个下标才是横坐标。
\[V = U_{21}(1-0.6)(1-0.4)+ U_{22}(1-0.4)(1-0.4)+ U_{31}(1-0.6)(1-0.6)+ U_{32}(1-0.4)(1-0.6)\]
(4) STN小结
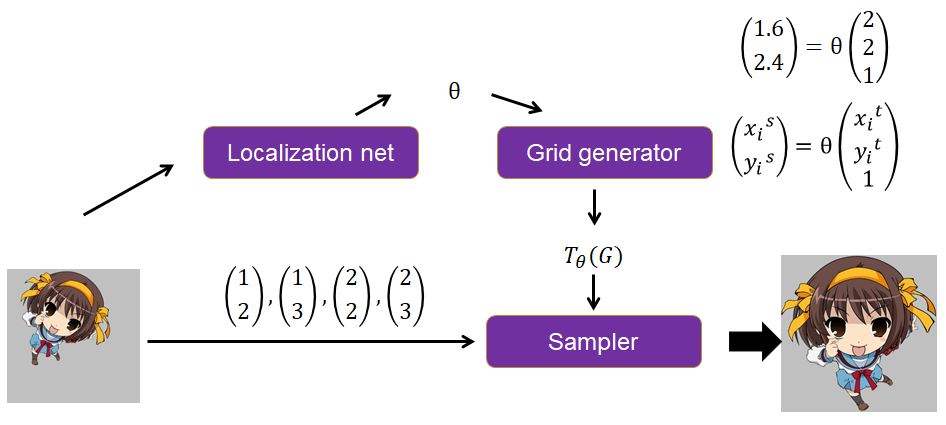
简单总结一下,如下图所示
- Localization net根据输入图,计算得到一个\(\Theta\)
- Grid generator根据输出图的坐标点和\(\Theta\),计算出输入图的坐标点,举例来说想知道输出图上(2,2)应该填充什么坐标点,则跟\(\Theta\)运算,得到(1.6,2.4)
- Sampler根据自己定义的填充规则(一般用双线性插值)来填充,比如(2,2)坐标对应到输入图上的坐标为(1.6,2.4),那么就要根据输入图上(1.6,2.4)周围的四个坐标点(1,2),(1,3),(2,2),(2,3)的像素值来填充。
【实验】Distorted MNIST

【实验】SVHN: Street View House Numbers

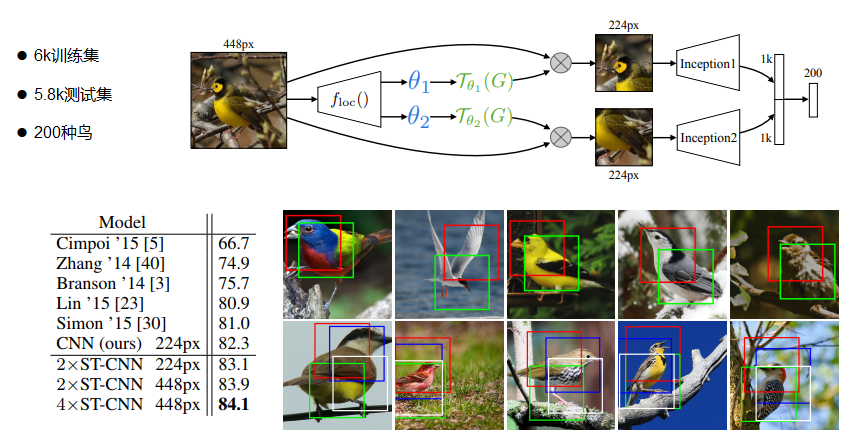
【 实验】CUB-200-2011 birds dataset
【附录】旋转的矩阵运算
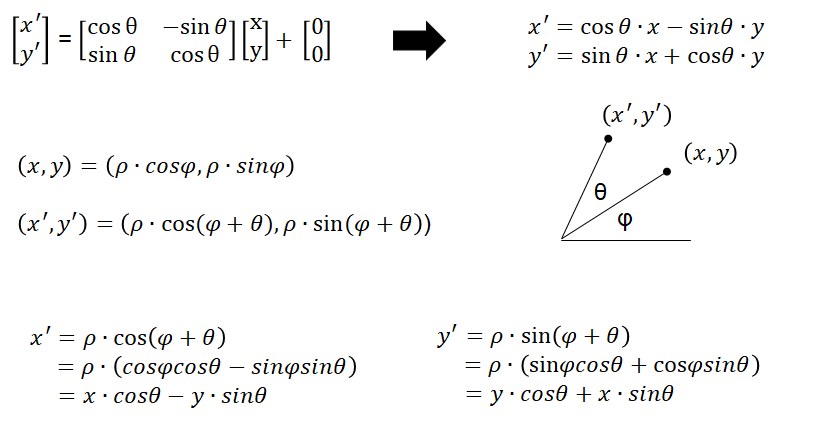
论文笔记:空间变换网络(Spatial Transformer Networks)的更多相关文章
- Spatial Transformer Networks(空间变换神经网络)
Reference:Spatial Transformer Networks [Google.DeepMind]Reference:[Theano源码,基于Lasagne] 闲扯:大数据不如小数据 这 ...
- [论文理解] Spatial Transformer Networks
Spatial Transformer Networks 简介 本文提出了能够学习feature仿射变换的一种结构,并且该结构不需要给其他额外的监督信息,网络自己就能学习到对预测结果有用的仿射变换.因 ...
- spatial transformer networks 这篇论文
大致看了看这个paper, 很novel. 我的观点: 在traditional convolutional neural netwoks 中,我们通常会depend 于 extracting fea ...
- 空间变换网络(STN)原理+2D图像空间变换+齐次坐标系讲解
空间变换网络(STN)原理+2D图像空间变换+齐次坐标系讲解 2018年11月14日 17:05:41 Rosemary_tu 阅读数 1295更多 分类专栏: 计算机视觉 版权声明:本文为博主原 ...
- 纯干货:深度学习实现之空间变换网络-part2
https://www.jianshu.com/p/854d111670b6 纯干货:深度学习实现之空间变换网络-part1 在第一部分中,我们主要介绍了两个非常重要的概念:仿射变换和双线性插值,并了 ...
- 深度学习方法(十二):卷积神经网络结构变化——Spatial Transformer Networks
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.机器学习技术感兴趣的同学加入. 今天具体介绍一个Google ...
- (转载)理解Spatial Transformer Networks
理解Spatial Transformer Networks 转载于:知乎-SIGAI 书的购买链接 书的勘误,优化,源代码资源 获取全文PDF请查看:理解Spatial Transformer Ne ...
- pytorch空间变换网络
pytorch空间变换网络 本文将学习如何使用称为空间变换器网络的视觉注意机制来扩充网络.可以在DeepMind paper 阅读更多有关空间变换器网络的内容. 空间变换器网络是对任何空间变换的差异化 ...
- STN(Spatial Transformer Networks)
url: https://arxiv.org/abs/1506.02025 year:2015 blog: https://kevinzakka.github.io/2017/01/10/stn-pa ...
随机推荐
- Js 的几种去重(一维)
写的几种数组去重方法: 第一种: [利用排序方法,然后比较当前元素与下一个元素是否相等] function repeat1(arr) { var length = arr.length; var re ...
- JavaScript 事件循环 — event loop
引言 相信所有学过 JavaScript 都知道它是一门单线程的语言,这也就意味着 JS 无法进行多线程编程,但是 JS 当中却有着无处不在的异步概念 .在初期许多人会把异步理解成类似多线程的编程模式 ...
- nginx的allow和deny配置
转自:http://www.ttlsa.com/linux/nginx-modules-ngx_http_access_module/ 单看nginx模块名ngx_http_access_module ...
- Freebsd下用pureftpd配置FTP服务器
pureftpd安装配置简明说明 1.下载 http://sourceforge.net/projects/pureftpd/ 最新版本是pure-ftpd-1.0.16a.tar.bz2 BSD自 ...
- Tortoise SVN 使用
1.添加文件或文件夹 2.删除文件或文件夹 ①If you want to delete an item from the repository, but keep it locally as an ...
- EntityFramework.DynamicFilters 实现软删除和租户过滤
EntityFramework.DynamicFilters 实现软删除和租户过滤
- INFORMATION_SCHEMA.STATISTICS 统计 表 库 大小
INFORMATION_SCHEMA MySQL :: MySQL 5.5 Reference Manual :: 21 INFORMATION_SCHEMA Tables https://dev.m ...
- mysql创建索引时报错1170
MySQL只能将BLOB/TEXT类型字段设置索引为BLOB/TEXT数据的前N个字符. 索引指定下col2的长度就可以了 :alter table foo add index col_2 (col2 ...
- 与python的第一次邂逅
python简介 一.什么是python python是一种面向对象.直译式的计算机程序语言,所以有了武老师的那句名言:一切皆为对象 python的设计哲学是:“优雅”,“明确”,“简单” pytho ...
- 【题解】P5151 HKE与他的小朋友
[题解]P5151 HKE与他的小朋友 实际上,位置的关系可以看做一组递推式,\(f(a_i)=f(a_j),f(a_j)=f(a_t),etc...\)那么我们可以压进一个矩阵里面. 考虑到这个矩阵 ...
