Loj 538 递推数列

Loj 538 递推数列

出题人:这题提高难度吧.于是放在了%你赛的 \(D1T2\) .

• 递推式为 \(a_i=k*a_{i-1}+a_{i-2}\) , 注意到 \(k\in \mathbb{N_+}\) ,容易发现一个比较显然的性质:

  若 \(a_i>a_{i-1}\geq 0\) , 或者 \(a_i<a_{i-1}\leq 0\) ,则该数列在第 \(i-1\) 项后单调上升或单调下降.

• 基于这个性质,一个比较自然的想法是,一直爆算 \(a_i\) ,使得数列 \(a\) 单调后退出,再利用单调性来算答案.

• 这样搞能得到多少分? \(20?\ 25?\ 30?\) 万一被构造数据卡到很久都进不了单调咋办?

• 事实上,这样计算可以获得 \(100\) 分的好成绩.借助下面这张图来分析,比例可能不太真实,意会即可.

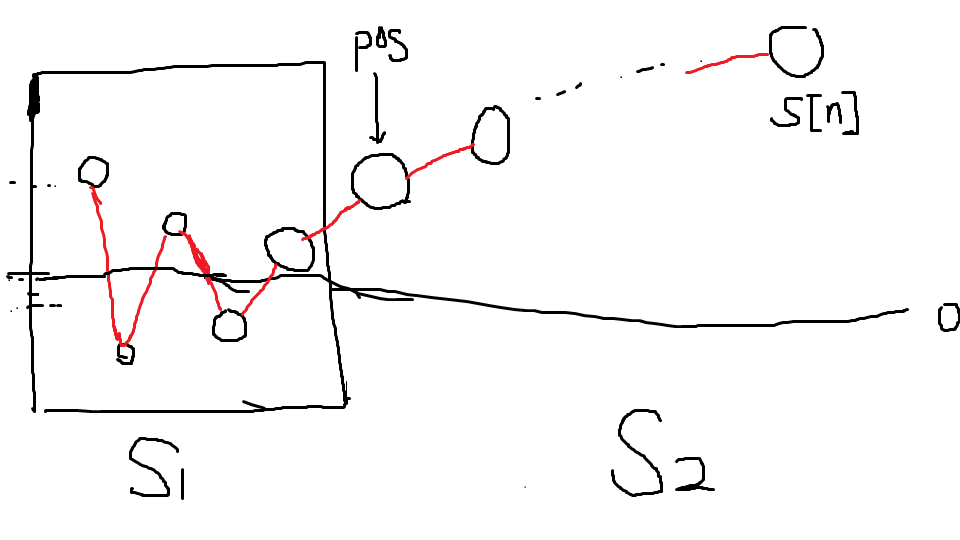
• 假定在 \(i=pos\) 处第一次满足 \(a_i>a_{i-1}\geq 0\) 或 \(a_i<a_{i-1}\leq 0\).那么 \(pos-1\) 之前的项都是正负交替出现的.否则若有 \(i<pos-1,0<a_i<a_{i-1}\) ,则 \(a_{i+1}>a_i>0\) , \(i+1<pos\) , 应是第一个找到的 \(pos\) ,矛盾.
• 那么记 \(b_i=|a_i|\) ,则有 \(\forall\ i\in [2,pos-1),b_i=-kb_{i-2}+b_{i-1}.\),且 \(b\) 单调递减.
• 移项变形,得 \(b_{i-2}=kb_{i-1}+b_i\geq(k+1)b_i\). 又因 \(k\in \mathbb{N_+}\) ,可得 \(pos\leq 2log_{k+1}|a_0|\) .
• 类似可以证明单调后在 \(O(loga)\) 个数内,绝对值将超过前面( \(S_1\) 内元素)的绝对值.
• 于是,整个算法的时间复杂度为 \(O(nloga)\) .实现起来细节比较多.

有时, \(yy\) 出一个做法或许并不难,难的是判断这个做法是否可行...