51nod 1943 联通期望 题解【枚举】【二进制】【概率期望】【DP】

集合统计类期望题目。

题目描述

在一片大海上有 \(n\) 个岛屿，规划建设 \(m\) 座桥，第i座桥的成本为 \(z_i\)，但由于海怪的存在，第 \(i\) 座桥有 \(p_i\) 的概率不能建造。

求在让岛屿尽量联通的情况下，期望最小成本为多少。

尽量联通：在对每座桥确定能否建造的情况下，对于任意两个岛屿，如果存在一种建桥方案使得它们联通，那么它们必须联通。

输入输出格式

输入格式：

第一行：两个整数 \(n\) 和 \(m\)（\(n\) 为岛屿数量，\(m\) 为桥的数量），中间用空格分割。

之后 \(m\) 行，每行三个整数 \(x_i,y_i,z_i\) 和一个实数 \(p_i\)，表示一条联通岛屿 \(x_i\) 与 \(y_i\) 的桥，成本为 \(z_i\)，有 \(p_i\) 的概率损坏。保证不存在重边。

输出格式：

一行，一个实数 \(ans\)，表示期望最小成本。输出保留6位小数。

输入输出样例

输入样例：

3 3
1 2 10 0.5
1 3 10 0.5
2 3 10 0.5

输出样例：

13.750000

说明

数据范围：

\(n\le 14,\ m\le \frac{n(n−1)}{2},\ z_i\le 100000,\ 0<p_i<1​\)

样例解释：

1. 有 \(\frac 18​\) 的概率能建 \(3​\) 座桥，那么尽量联通的最小代价是 \(20​\)。

2. 有 \(\frac 38​\) 的概率能建 \(2​\) 座桥，那么尽量联通的最小代价是 \(20​\)。

3. 有 \(\frac 38​\) 的概率能建 \(1​\) 座桥，那么尽量联通的最小代价是 \(10​\)。

4. 有 \(\frac 18​\) 的概率能建 \(0​\) 座桥，那么尽量联通的最小代价是 \(0​\)。

因此，总代价\(=\frac{1\times 20+3\times 20+3\times 10+0}8=13.750000\)。

题解：

集合一类的题目比较抽象，所以转移方程也有些难想。

首先我们考虑一条边在什么情况下会做出贡献。

理解题目中“尽量连通”的意思。对于一张图，如果两个点在原图上连通，那么要求他们在新图上必须连通。也就是求出最小生成森林。

因为相同权值的不同边对最小生成森林的最终结果互不影响，所以我们可以认为它们互不相同，对我们接下来的算法流程有一定的简化。首先按 \(z_i\) 排序，相同的 \(z_i\) 以下标为第二关键字。

那么一条边产生贡献当且仅当

• 它没有被破坏：\(1-p_i​\)，
• 不存在一条比它小的边连接 \(x_i,y_i​\)。

令 \(f[S]\) 表示集合 \(S\) 是当前的一个极大最小生成树的概率。极大最小生成树表示不存在一条边 \(\left<u,v\right>\) 使得 \(u\in S,v\notin S\) 且 \(S​\) 内部互相连通。

对于一条边 \(\left<x_i,y_i\right>​\)，枚举 \(x_i\in S,y_i\in T​\) 的集合 \(S​\) 和 \(T​\)，且 \(S\cap T=\varnothing​\)，则 \(f[S\cup T]​\) 的值与当前边就有了关系。如果之前没有连通，那么这条边会造成一个新的贡献；如果之前连通了，则不造成影响。所以 \(f[S\cup T]​\) 是加和关系。方程为 \(f[S\cup T]=f[S\cup T]+f[S]\times f[T]\times P\times (1-p_i)​\)，其中 \(P​\) 是一个参数，表示重复计算的一些量，在下面会重提。

当这条边被摧毁时，二者均不变。方程表示为 \(f[S]=f[S]\times p_i\)，这里没有上面的 \(P\)，原因在于当 \(f[S]\) 这个值有意义时，就代表之前全部都合法。

此时我们进一步讨论“如果之前没有连通”的情况。事实上不连通只要满足 \(S\cap T=\varnothing\) 就可以了，看上去是直接贡献到答案的，但是需要考虑一些特殊的边。

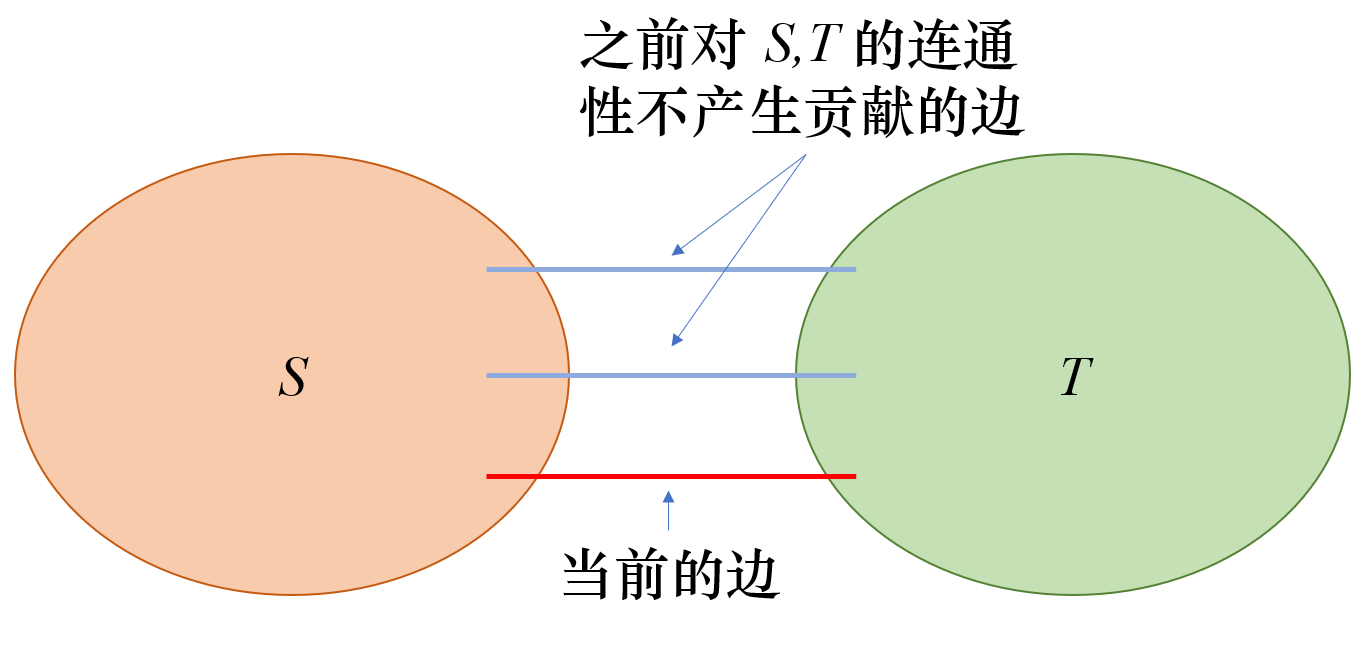
假设当前的边是红色，已经枚举到了 \(S,T\) 这两个集合。那么上面的蓝色边被摧毁时，分别在 \(S\) 和 \(T\) 处乘了 \(p_i\)，但是实际上这样的边每条只出现了一次。因此在合并的时候我们要把它除掉，令 \(g[S][T]\) 表示

\[\frac{\prod_{\left<u,v\right>\in E,u\in S,v\in T}p_{\left<u,v\right>}}{p_i}
\]

就是蓝色边的 \(p\) 的乘积。那么对于一条边以及它两边的集合 \(S,T\)，它的 \(P=g[S][T]\)，对答案的贡献就是 \(f[S]\times f[T]\times P\times (1-p_i)\times z_i\)。

此时考虑怎么算 \(g[S][T]\)，你甚至无法开下一个 \(2^{28}\) 大小的数组。但是这个数可以 \(O(1)\) 计算或每次动态维护，这里给出 \(O(1)\) 的计算方法。

令 \(h[S]\) 表示 \(S\) 内部没有点互相连通的概率。对于第 \(i\) 条边，还是枚举左右的集合 \(S,T\)。\(h[S\cup T]\) 仍不连通的概率是 \(h[S\cup T]\times p_i\)，注意这里和 \(h[S],h[T]\) 都没有关系。直观上理解是因为 \(S\) 和 \(T\) 之间可能还有一些边连接了，理性上分析原因是 \(h[S\cup P]\) 如果仍不连通，那么之前一定不连通，同时当前这条边也没有做出贡献。（就这么简单）

然后发现 \(h[S\cup T]\) 中的概率也是蓝色的边多算了一次，因此 \(g[S][T]=\frac{h[S\cup T]}{h[S]\times h[T]}\)。然后枚举计算就可以了。

同时要注意 \(f​\) 要满足无后效性，所以在更新完答案和一些无关的 \(f,h​\) 后再更新一些不影响的 \(f[S]=f[S]\times p_i​\)。

做了几个期望题..感觉到只要有任何一处细节错误就是 \(100\to 0\) 的节奏啊..省选应该不会主动开概率题的吧...

注意除法的常数极大，尽量转为乘法或者提前计算多次用到的数据。

由于枚举子集的子集复杂度为 \(O(3^n)\)，所以总时间复杂度是 \(O(m\cdot 3^{n-2})\)（题解说的。

\(O(2^{|S|})\) 枚举子集的方法可见博客置顶帖。

Code：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define db double
struct edge
{
    int x,y,z;
    db p;
    friend bool operator <(edge a,edge b)
    {return a.z<b.z;}
}e[300];
db f[1<<14],h[1<<14];
//h是完全不连通概率
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        scanf("%d%d%d%lf",&e[i].x,&e[i].y,&e[i].z,&e[i].p);
        --e[i].x;
        --e[i].y;
    }
    std::sort(e+1,e+1+m);
    for(int i=0;i<n;++i)
        f[1<<i]=1;
    for(int i=0;i<(1<<n);++i)
        h[i]=1;
    int U=(1<<n)-1;
    db ans=0;
    for(int i=1;i<=m;++i)
    {
        int x=1<<e[i].x,y=1<<e[i].y;
        int s=U^x^y;
        for(int j=s;j>=0;j=s&(j-1))
        {
            int t=U^j^x^y;
            for(int k=t;k>=0;k=t&(k-1))
            {
                db g=f[j|x]*f[k|y]*(1-e[i].p)/h[j|x|k|y]*h[j|x]*h[k|y];
                f[j|x|k|y]+=g;
                ans+=g*e[i].z;
                h[j|x|k|y]*=e[i].p;
                if(!k)
                    break;
            }
            if(!j)
                break;
        }

        for(int j=s;j>=0;j=s&(j-1))
        {
            f[j|x]*=e[i].p;
            f[j|y]*=e[i].p;
            if(!j)
                break;
        }
    }
    printf("%.6lf\n",ans);
    return 0;
}