377. Combination Sum IV 返回符合目标和的组数

［抄题］：

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.

Example:

nums = [1, 2, 3]
target = 4

The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

Note that different sequences are counted as different combinations.

Therefore the output is 7.

[暴力解法]：

时间分析：

空间分析：

[优化后]：

时间分析：

空间分析：

［奇葩输出条件］：

［奇葩corner case］：

DFS的退出条件每次都要走一遍，如果是计数类就不能清0了，应该返回1

［思维问题］：

［一句话思路］：

就是用dfs一直把所有方法加上就行了

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

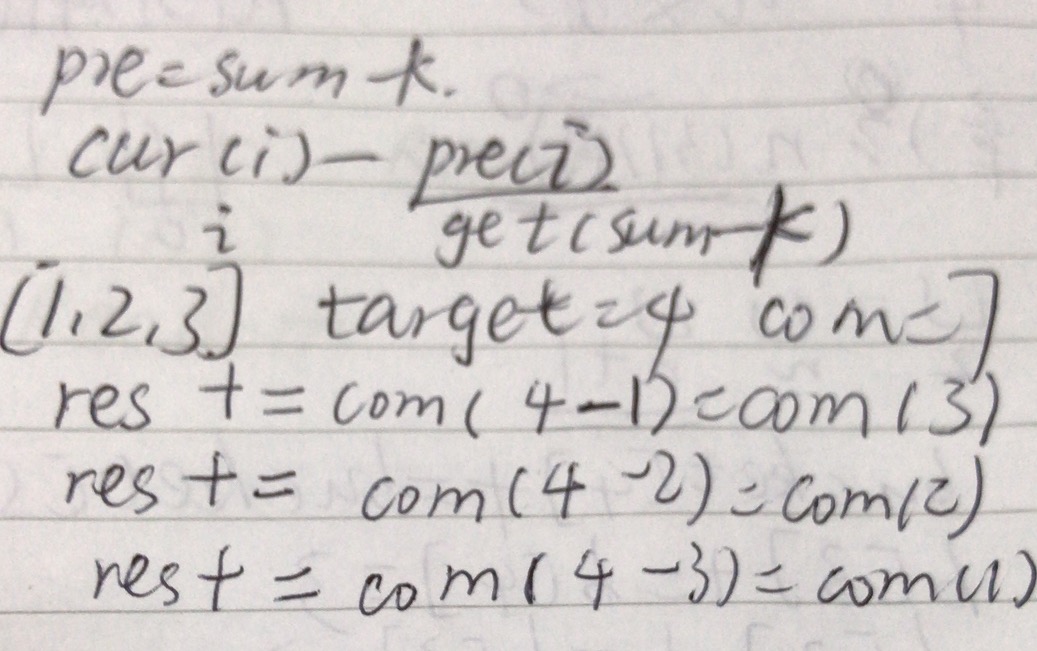
［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

DFS的退出条件每次都要走一遍，如果是计数类就不能清0了，应该返回1

［复杂度］：Time complexity: O(1^n) Space complexity: O(1)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［算法思想：递归/分治/贪心］：递归

［关键模板化代码］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public int combinationSum4(int[] nums, int target) {
    if (target == 0) {
        return 1;
    }
    int res = 0;
    for (int i = 0; i < nums.length; i++) {
        if (target >= nums[i]) {
            res += combinationSum4(nums, target - nums[i]);
        }
    }
    return res;
}