c 浮点数

一、二进制小数

　　十进制小数： 12.34₁₀ == 1 * 10¹ + 2 * 10⁰ + 3 * 10^-1 + 4 * 10^-2 = 12(34/100)　

　　（可能很多人还不知道怎么计算一个数的负幂，这里给大家一个方法：一个数的负的X次方等于这个数的X次方分之一，比如2^-2 = 0.25 = 1/2*2 = 1/4，现在明白不？）　

　　二进制小数：101.11 == 1 * 2² + 0 * 2¹ + 1 * 2⁰ + 1 * 2^-1 + 1 * 2^-2 = 4 + 0 + 1 + 1/2 + 1/4 = 5(3/4)

　　从二进制小数可以看出点左边的位的权是2的正幂；而点右边的位是2的负幂

　　下图是数b的定义：

　　

　　从该图中不难看出有两种情况：

　　　　a>. 把小数点向左移动一位的时候相当于这个数被除以2（比如：101.11₂ = 5.75 --- 往左移动一位 -->10.111₂ = 1 * 2² + 0 * 2¹ + 1 * 2^-1 + 1 * 2^-2 +1 * 2^-3 = 2 + 0 + 1/2 + 1/4 + 1/8 = 2(7/8) = 2.875,）

　　　　b>. 把小数点向右移动一位的时候相当于这个数被乘于2（比如：101.11₂ = 5.75 --- 往左移动一位 -->1011.1₂ = 1 * 2³ + 0 * 2² + 1 * 2¹ + 1 * 2⁰ +1 * 2^-1 = 8 + 0 + 2 + 1 + 1/2 = 11（1/2） = 11.5）

　　注意：

　　　　a>. 比如0.1,1111₂这样的数，刚好小于1，这样的数表示(63/64),我们使用科学计数法来表示：1.0-€

　　　　b>. 比如1/3、5/7这样的数，就是二进制小数所表单不了的，二进制小数表示法只能表示那些能够被写成x * 2^y 的数

　　下面是一些题目，咱们借着题目分析一下（这个题目是深入理解计算机系统第三版的练习题）：

　　

　　疑问：

　　　　1.如何知道二进制小数部分有几位小数？ 答：看分母，将分母换算成二进制，得到n位二进制数再减1（8 = 1000 = 4-1 = 3），比如1/8 = 0.001、1/2 = 0.1、1/16 = 0.0001

　　　　2.分子换算成小数部分后从小数点往右 位权越大还是越小？ 答：从小数点往右二进制位的权越来越小，比如：1/16 =0.0001（有人计算出来是0.1000，这样是错的，这样的结果就是8/16 = 1/2 = 0.5 = 5 * 10^-1 = 5/10 = ）-------->这里涉及到十进制小数转二进制小数的问题，就是用小数去乘以2，不断的取整数：0.5 * 2 = 1.0 取1，小数部分就是1，结果就是0.1，一直乘以2，知道结果为1.0位置

　　a>. 3/8，首先分子比分母小，结果小于1；分母为8抓成二进制1000，小数部分则是n-1 = 3，分子部分011(是从右往左的)，结果就是0.011；十进制：0.(1 * 2^-2 + 1 * 2^-3) = 3/8 = 0.375

　　b>. 23/16，首先分子大于分母，结果大于1，先计算整数部分为1，剩余为7/16，确定几位小数16 = 10000，小数位n-1 = 4，分子转成4位二进制 = 0111，结果就是1.0111；十进制：1 * 2^0 + 1 * 2^-2 + 1 * 2^-3  + 1 * 2^-4 = 1 + 0.25 + 0.125 + 0.0625 = 1.4375

　　c>. 10.1101,逆向运算 1 * 2^1 + 1 * 2^-1 + 1 * 2^-2 + 1 * 2^-4 = 2 + 1/2 + 1/4 + 1/16 = 2 + 13/16 = 45/16;十进制：2.8125

　　d>. 1.011 === 1 * 2^1 + 1 * 2^-2 + 1 * 2^-3 = 1 + 4/8 + 1/8 = 13/8 = 1.625

　　e>. 5.375 首先整数部分是5 = 101，小数部分是0.375，按照十进制小数转二进制小数，不断乘2，取整数（011），小数部分是011，结果就是101.011;小数值：5（3/8） = 43/8

　　f>.3.0625 首先整数部分是3 = 11，小数部分0.0625 = 0001，结果就是11.0001；小数值：3（1/16） = 49/16

二、IEEE浮点表示

　　IEEE浮点标准（表示一个数）：V = （-1）^s * M * 2^E (不太理解)

　　介绍：

　　　　符号（s）：决定数是负数（s == 1）还是整数（s == 0），而对于数值0的符号位解释作为特殊情况处理

　　　　有效数（M）：它是一个二进制小数，它的范围在1~2-€或者0~1-€之间

　　　　指数（E）：2的幂（正负都有可能），它的作用是对浮点数加权

　　浮点数的位分为三个域，编码值：

　　　　符号位（s）：决定正负

　　　　尾数（M）：一个二进制小数

　　　　阶码（E）：对浮点数加权

　　存储一个浮点数（s正负号、exp指数E，frac小数部分）：

　　　　对于单精度浮点格式(32位)：

　　　　　　

　　　　对于双精度浮点格式(64位)：

　　　　　　

　　根据阶码（E）字段的值不同我们可以分为四类浮点数：

　　a>. 规格化浮点数：

　　　　

　　　　规格化浮点数：阶码值E = e - bias（2^k-1 -1）,bias在单精度情况下是127，双精度情况下是1023，因此单精度下E的值为[-126~+127]，在双精度下E的值为[-1022~+1023]；对于小数字段frac，f =0. f_n-1f_n-2.....f₀,而位数M = f +1；在这里我们将浮点数的首位默认为1，所以没有显示的存储在存储器中，为什么能这样呢？因为我们可以通过调整阶码值E，使小数部分二进制的值落在1~2之间，获得额外的精度为

　　　　例如：0.10111，存储的话小数部分的二进制位是5位，存储就是000...10111，但是浮点数首位默认为1之后，我们小数部分存4位就可以了，1.0111 * 2^-1 （why？？前面咱们提到过，二进制小数，小数点往左移动一位就是除以2，往右移动就是乘以2，在这里我们往右移动了一位，结果就是1.0111,那么我们还原回去保持值不变就必须除以2，也就是*1/2）

　　　　表示范围：单精度下[-2^127,2^127]，双精度下[-2^1023,2^1023]，那么规范化的绝对值是大于 2 ^ (-126) 或 2 ^ (-1022) 的数字

　　　　示例1:0.25，先转成二进制小数0.01,那么根据规范化的属性转换一种形式，小数点往右移动2位 (0.01 * 2^2) * 2^-2 = 1.0 * 2^-2，根据阶码值计算E = -2 + 127 = 125，二进制小数部分全部都是0，那么最后的结果就是0 0111 1101 0000 0000 0000 0000 0000 000

　　　　示例2:1.5，转成二进制1.1，规格化默认首位为1，先忽略，0.1 * 2^0，那么阶码E = 127 + 0 = 127 = 01111111，小数部分1，后边补齐0即可，结果就是0 0111 1111 1000 0000 0000 0000 0000 000

　　b>. 非规格化浮点数：

　　　　

　　　　非规格化浮点数：定义阶码E = 1 - bias （2^k-1 -1），M = f = 0.fn-1 fn-2 fn-3 …… f2 f1 f0

　　　　表示范围：非规范化浮点数表示的则是小于 2 ^ (-126) 或 2 ^ (-1022) 的值

　　c>. 无穷大：

　　　　

　　　　无穷大：frac部分二进制小数全为0

　　d>. NaN（Not a Number）

　　　　

　　　　NaN：frac部分二进制小数不全为0

　　下边是几个文章的链接(写的特别好)：

　　　　http://blog.csdn.net/hqin6/article/details/6701109

　　　　http://www.atjiang.com/CSAPP3-2.4_floating_point/

　　　　https://yasicyu.com/newarticle/IEEE-754%E6%A0%87%E5%87%86%E4%B8%8E%E5%AE%9E%E7%8E%B0

　　下面是一些练习题，本人对这一部分不是很懂，所以记录一下面试题的分析过程：

　　　　IEEE浮点格式的5位浮点数表示，1位符号位、2个指数位(k=2)和2位小数，指数偏移量bias = 2^k-1 - 1 = 1

　　　　

　　　　

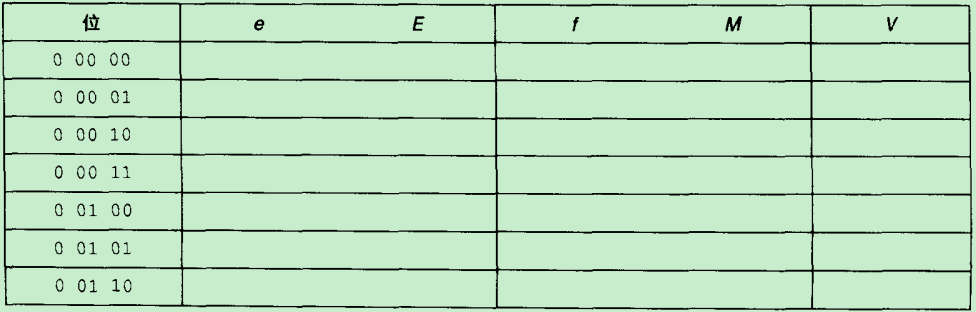
　　　　注意（0 00 00）：

　　　　　　1.IEEE754浮点数表达式： V = M * 2^e  bias = 2k-1 - 1 = 1

　　　　　　2. 规格化数：E = e - Bias = e - 2^k-1 - 1；M = f + 1

　　　　　　2.1 规格化数的范围：小数部分 0+1 = 1 ~ 1+3/4 = 7/4， V的范围 1 * 2^-1 = 1/2 ~ 2 * 7/4 = 14/4

　　　　　　3.非规格化数：E = 1 - Bias = 1 - 2^k-1 - 1；f = M

　　　　　　3.1.非规格化数的范围：小数部分 0 ~ 3/4；阶码值为0，V的范围0 ~ 3/4

　　　　开始做题：

　　　　　　a>. 0 00 00: e = 0; E = 1-bias = 0; f = 0; M = 0; V = 0;

　　　　　　b>. 0 00 01: e = 0; E = 0; f = 1/4; M = f = 1/4; V = 1/4 * 2^0 = 1/4

　　　　　　c>. 0 00 10: e = 0; E = 0; f = 2/4; M = f = 2/4; V = 2/4 * 2^0 = 2/4

　　　　　　d>. 0 00 11; e = 0; E = 0; f = 3/4; M = f = 3/4; V = 3/4 * 2^0 = 3/4

　　　　　　e>. 0 01 00(这个就不再是非规格化数了，非规格化数的特点是阶码值全为0，这个符合规格化数)：e = 1; E = e - Bias = 1 - 1 = 0; f = 0; M = f + 1 = 4/4; V = 2^0 * 4/4 = 4/4

　　　　　　f>.  0 01 01: e = 1; E = 0; f = 1/4; M = f + 1 = 5/4; V = 2^0 * 5/4 = 5/4

　　　　　　g>. 0 01 10: e = 1; E = 0; f = 2/4; M = f + 1 = 6/4; V = 2^0 * 6/4 = 6/4

　　　　　　h>. 0 01 11: e = 1; E = 0; f = 3/4; M = f + 1 = 7/4; V = 2^0 * 7/4 = 7/4

　　　　　　i>. 0 10 00: e = 2; E = 1; f = 0; M = f + 1 = 4/4; V = 2^1 * 4/4 = 8/4

　　　　　　j>. 0 10 01: e = 2; E = 1; f = 1/4; M = f +1 = 5/4; V = 2^1 * 5/4 = 10/4

　　　　　　k>. 0 10 10: e = 2; E = 1; f = 2/4; M = f +1 = 6/4; V = 2^1 * 6/4 = 12/4

　　　　　　l>. 0 10 11: e = 2; E = 1; f = 3/4; M = f + 1 = 7/4; V = 2^1 * 7/4 = 14/4

　　　　　　m>. 0 11 00 :这种情况就是无穷大的情况，因为阶码值全是1，小数部分全是0

　　　　　　n>. 0 11 01: 这种情况就是NaN了，因为阶码值全是1，而小数部分不全是0（e = 3; E = 2; f = 1/4; M = f + 1 = 5/4; V = 2^2 * 5/4 = 20/4 > 14/4）

三、浮点数舍入

　　浮点数舍入有四种方法，默认的舍入方法：向偶数舍入（round-to-even），也被称为向最接近的值舍入；其他三种方法产生的实际值的确界；

　　　　向偶数舍入：它试图找到最接近的值，采用的方法是将数字向上或者向下舍入，使得结果的最低有效位是偶数

　　　　　　比如：1.5RMB、2.5RMB想偶数舍入的结果都是2RMB

　　　　向零舍入：正数向下舍入，负数向上舍入，|x^| <= |x|

　　　　向下舍入：把正数和负数都向下舍入，x^- < x

　　　　向上舍入：吧正数和负数都向上舍入，x⁺ > x

四、浮点数运算

　　浮点数不具有结合性

　　对于任何x，都有NaN + x = NaN

　　浮点数满足单调性熟属性：a>=b ,对于任何a,b的值，除了x不等于NaN，都有x + a >= x + b

五、浮点数

　　int、float、double三个类型相互转换：

　　a>. int转float，数值不会溢出，可能会被舍去

　　b>. int、float转double，因为double的范围更大，也有更高的位数(更多的有效位)，能够保留精确的值

　　c>.double转float,从大范围转成小范围，所以值可能会溢出成+∞或-∞，由于精度较小，可能会被舍去

　　d>. double、float转int值将会向0截断，比如1.9999将会等于1，-1.99999将会等于-1