Discrete Logging(POJ2417 + BSGS)

题目链接：http://poj.org/problem?id=2417

题目：

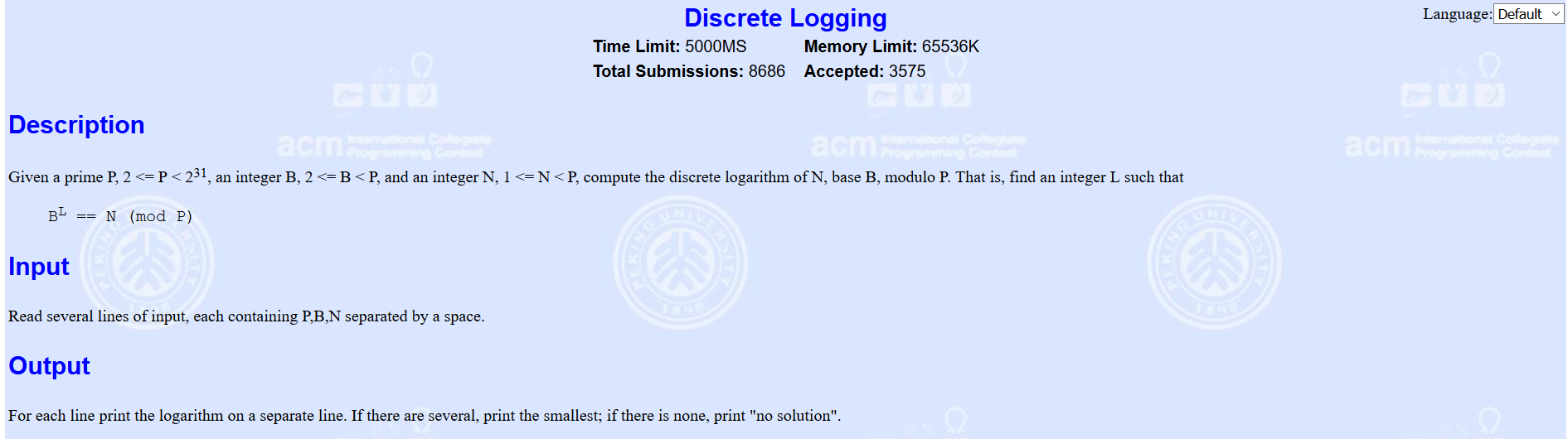
题意：

　　求一个最小的x满足a^x==b(mod p)，p为质数。

思路：

　　BSGS板子题，推荐一篇好的BSGS和扩展BSGS的讲解博客：http://blog.miskcoo.com/2015/05/discrete-logarithm-problem

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pli;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson i<<1
 #define rson i<<1|1
 #define lowbit(x) x&(-x)
 #define bug printf("*********\n");
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e9 + ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3f;

 int a, b, p;

 struct Hashmap { //哈希表
     static const int Ha=, maxe=;
     int E,lnk[Ha], son[maxe+], nxt[maxe+], w[maxe+];
     int top, stk[maxe+];
     void clear() {
         E=;
         while(top) lnk[stk[top--]]=;
     }
     void Add(int x,int y) {
         son[++E]=y;
         nxt[E]=lnk[x];
         w[E]=((<<) - ) *  + ;
         lnk[x]=E;
     }
     bool count(int y) {
         int x=y % Ha;
         for (int j = lnk[x]; j; j=nxt[j])
             if (y == son[j]) return true;
         return false;
     }
     int& operator [] (int y) {
         int x=y % Ha;
         for (int j = lnk[x]; j; j = nxt[j])
             if (y == son[j]) return w[j];
         Add(x,y);
         stk[++top]=x;
         return w[E];
     }
 }mp;

 int exgcd(int a, int b, int& x, int& y) {
     if(b == ) {
         x = , y = ;
         return a;
     }
     int d = exgcd(b, a % b, x, y);
     int t = x;
     x = y;
     y = t - a / b * y;
     return d;
 }

 int BSGS(int A, int B, int C) {
     if(C == ) {
         if(!B) return A != ;
         else return -;
     }
     if(B == ) {
         if(A) return ;
         else return -;
     }
     if(A % C == ) {
         if(!B) return ;
         else return -;
     }
     int m = ceil(sqrt(C));  //分块
     int D = , base = ;
     mp.clear();
     for(int i = ; i <= m - ; i++) {
         if(mp[base] == ) mp[base] = i;
         else mp[base] = min(mp[base], i);
         base = ((LL)base * A) % C;
     }
     for(int i = ; i <= m - ; i++) {
         int x, y, d = exgcd(D, C, x, y);
         x = ((LL)x * B % C + C) % C;
         if(mp.count(x)) return i * m + mp[x];
         D = ((LL)D * base) % C;
     }
     return -;
 }

 int main() {
     //FIN;
     while(~scanf("%d%d%d", &p, &a, &b)) {
         int ans = BSGS(a, b, p);
         if(ans == -) printf("no solution\n");
         else printf("%d\n", ans);
     }
     return ;
 }