【10.3校内测试【国庆七天乐！】】【DP+组合数学/容斥】【spfa多起点多终点+二进制分类】

最开始想的暴力DP是把天数作为一个维度所以怎么都没有办法优化，矩阵快速幂也是$O(n^3)$会爆炸。

但是没有想到另一个转移方程：定义$f[i][j]$表示每天都有值的$i$天，共消费出总值$j$的方案数。然后答案就是。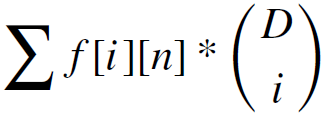

所以每次维护前缀和就可以$O(1)$转移了。

注意前缀和的初值。

#include<bits/stdc++.h>
#define LL long long
#define mod 998244353
using namespace std;

int n, m;
LL d;
LL dp[][], sum[][];

LL mpow(LL a, LL b) {
    LL ans = ;
    for(; b; b >>= , a = a * a % mod)
        if(b & )    ans = ans * a % mod;
    return ans;
}

LL rev(LL a) {
    return mpow(a, mod - );
}

LL comb(LL p, int q) {
    LL a = , b = ;
    for(LL i = p - q + ; i <= p; i ++)
        a = i % mod * a % mod;
    for(int i = ; i <= q; i ++)
        b = b * i % mod;
    LL ans = a * rev(b) % mod;
    return ans;
}

int main() {
    freopen("contract.in", "r", stdin);
    freopen("contract.out", "w", stdout);
    while(cin >> n >> d >> m) {
        if(n ==  && d ==  && m == )    break;
        d %= mod;
        int now = ;
        memset(sum, , sizeof(sum));
        memset(dp, , sizeof(dp));
        for(int i = ; i < m && i <= n; i ++)
            dp[][i] = ;
        for(int i = ; i <= n; i ++)
            sum[][i] = sum[][i-] + dp[][i];
        for(int i = ; i <= n && i <= d; i ++) {
            for(int j = ; j <= n; j ++) {
                if(j - m > )    dp[i][j] = (sum[i-][j-] - sum[i-][j-m] + mod) % mod;
                else dp[i][j] = sum[i-][j-];
                sum[i][j] = (sum[i][j-] + dp[i][j]) % mod;
            }
        }
        LL ans = ;
        for(int i = ; i <= n && i <= d; i ++) {
            LL tmp = comb(d, i);
            ans = (ans + tmp * dp[i][n] % mod) % mod;
        }
        printf("%lld\n", ans);
    }
    return ;
} 

起点确定的最小环。

我们可以发现，因为环的起点和终点都是1，所以题目实际是找与1相连的一个起点和一个终点（因为要保证没有走重边，所以起点和终点一定不同），而对于两个不同的数，二进制位上一定有至少一位不相同，所以可以按每一位，将二进制中当前位不同的点分成两组，代表当前起点和终点，每次跑一遍多起点多终点的$Spfa$，统计最小答案即可。

【注意】不能把每次跑完得到的起点终点直接两两配对，因为两点不一定能相互到达，还是应该在$Spfa$中赋初值跑完。

#include<bits/stdc++.h>
#define oo 0x3f3f3f3f
using namespace std;

int n, m, tot;

struct Node {
    int u, v, nex, w;
    Node(int u = , int v = , int nex = , int w = ) :
        u(u), v(v), nex(nex), w(w) { }
} Edge[];

int stot, h[];
void add(int u, int v, int s) {
    Edge[++stot] = Node(u, v, h[u], s);
    h[u] = stot;
}

int vis[], dis[], S[], T[], nums, numt, W[], rt[];
queue < int > q;
void Spfa() {
    memset(vis, , sizeof(vis));
    memset(dis, 0x3f3f3f3f, sizeof(dis));
    for(int i = ; i <= nums; i ++)    q.push(S[i]), vis[S[i]] = , dis[S[i]] = W[S[i]];
    while(!q.empty()) {
        int x = q.front(); q.pop(); vis[x] = ;
        for(int i = h[x]; i; i = Edge[i].nex) {
            int v = Edge[i].v;
            if(dis[v] > dis[x] + Edge[i].w && v != ) {
                dis[v] = dis[x] + Edge[i].w;
                if(!vis[v]) {
                    vis[v] = ;    q.push(v);
                }
            }
        }
    }
}

int main() {
    freopen("leave.in", "r", stdin);
    freopen("leave.out", "w", stdout);
    int t;
    scanf("%d", &t);
    while(t --) {
        scanf("%d%d", &n, &m);
        stot = , tot = ;
        memset(h, , sizeof(h));
        memset(W, , sizeof(W));
        memset(rt, , sizeof(rt));
        int ans = 0x3f3f3f3f;
        for(int i = ; i <= m; i ++) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c);    add(b, a, c);
            if(b < a)    swap(a, b);
            if(a == ) rt[++tot] = b, W[b] = c;
        }
        if(tot <= ) {
            printf("-1\n"); continue;
        }
        sort(rt + , rt +  + tot);
        int M = rt[tot];
        int tmp = ;
        while(M) {
            memset(S, , sizeof(S));
            memset(T, , sizeof(T));
            nums = ; numt = ;
            int t = M & ;
            for(int i = ; i <= tot; i ++)
                if(((rt[i] >> tmp) & ) == t)    S[++nums] = rt[i];
                else    T[++numt] = rt[i];
            Spfa();
            for(int i = ; i <= numt; i ++)
                ans = min(ans, W[T[i]] + dis[T[i]]);
            M >>= ; tmp ++;
        }
        if(ans < oo)    printf("%d\n", ans);
        else printf("-1\n");
    }
    return ;
}