[P1768]天路(分数规划+SPFA判负环)

题目描述

“那是一条神奇的天路诶~，把第一个神犇送上天堂~”，XDM先生唱着这首“亲切”的歌曲，一道猥琐题目的灵感在脑中出现了。

和C_SUNSHINE大神商量后，这道猥琐的题目终于出现在本次试题上了，旨在难到一帮大脑不够灵活的OIer们（JOHNKRAM真的不是说你……）。

言归正传，小X的梦中，他在西藏开了一家大型旅游公司，现在，他要为西藏的各个景点设计一组铁路线。但是，小X发现，来旅游的游客都很挑剔，他们乘 火车在各个景点间游览，景点的趣味当然是不用说啦，关键是路上。试想，若是乘火车一圈转悠，却发现回到了游玩过的某个景点，花了一大堆钱却在路上看不到好 的风景，那是有多么的恼火啊。

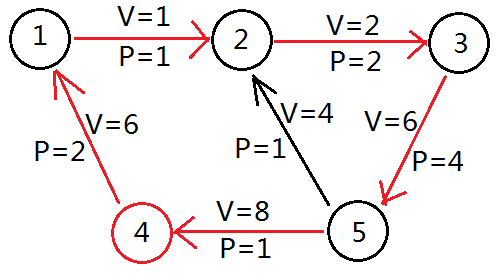
所以，小X为所有的路径定义了两个值，Vi和Pi，分别表示火车线路的风景趣味度和乘坐一次的价格。现在小X想知道，乘客从任意一个景点开始坐火车 走过的一条回路上所有的V之和与P之和的比值的最大值。以便为顾客们推荐一条环绕旅游路线（路线不一定包含所有的景点，但是不可以存在重复的火车路线）。

于是，小X梦醒之后找到了你……

输入输出格式

输入格式：

第一行两个正整数N，M，表示有N个景点，M条火车路线，火车路线是单向的。

以下M行，每行4个正整数，分别表示一条路线的起点，终点，V值和P值。

注意，两个顶点间可能有多条轨道，但一次只能走其中的一条。

输出格式：

一个实数，表示一条回路上最大的比值，保留1位小数。

若没有回路，输出-1。

输入输出样例

输入样例#1：
复制

5 6
1 2 1 1
4 1 6 2
5 4 8 1
2 3 2 2
5 2 4 1
3 5 6 4

输出样例#1： 复制

2.3

说明

对于30%的数据，1≤N≤100,1≤M≤20;

对于60%的数据，1≤N≤3,000,1≤M≤2,000;

对于100%的数据，1≤N≤7,000,1≤M≤20,000,1≤Vi,Pi≤1,000.

保证答案在200以内.

分数规划裸题（主要是得想到这个算法），分数规划实际上就是移项之后的二分答案。

二分之后SPFA判负环即可，注意要用DFS版的SPFA（这么重要的算法我以前竟然毫无所知）

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define rep(i,l,r) for (int i=l; i<=r; i++)
 using namespace std;

 const int N=;
 struct P{ int to,nxt; double v1,v2; }e[N<<];
 int n,m,u,v,len,h[N],vis[N],flag;
 double w1,w2,dis[N];

 void spfa(double now,int x){
     if (flag) return;
     vis[x]=;
     for (int i=h[x],k; i; i=e[i].nxt)
         if (dis[k=e[i].to]>dis[x]+now*e[i].v2-e[i].v1){
             dis[k]=dis[x]+now*e[i].v2-e[i].v1;
             if (!vis[k]) spfa(now,k); else { flag=; return; }
         }
     vis[x]=;
 }

 bool check(double now){
     flag=;
     memset(dis,,sizeof(dis));
     memset(vis,,sizeof(vis));
     rep(i,,n){
         spfa(now,i);
         if (flag)break;
     }
     if (flag) return ; return ;
 }

 int main(){
     scanf("%d %d",&n,&m);
     rep(i,,m){
         scanf("%d %d %lf %lf",&u,&v,&w1,&w2);
         e[++len].to=v; e[len].v1=w1; e[len].v2=w2; e[len].nxt=h[u]; h[u]=len;
     }
     double l=,r=200.0,mid;
     while (l+0.01<r){
         mid=(l+r)/;
         if (check(mid))l=mid; else r=mid;
     }
     if (l==) printf("-1"); else printf("%.1lf",r);
     return ;
 }