数据结构和算法 – 9.二叉树和二叉查找树

 

9.1.树的定义

 

9.2.二叉树

人们把每个节点最多拥有不超过两个子节点的树定义为二叉树。由于限制子节点的数量为 2，人们可以为插入数据、删除数据、以及在二叉树中查找数据编写有效的程序了。

在考虑一种更加特殊的二叉树——二叉查找树的时候，鉴别子节点是很重要的。二叉查找树是一种较小数据值存储在左节点内而较大数据值存储在右节点内的二叉树。正如即将看到的那样，这种属性可以使查找非常有效。

 

9.2.1.构造二叉查找树

二叉查找树由节点组成，所以需要一个 Node 类，这个类类似于链表实现中用到的 Node 类。

    public class Node
    {
        public int Data;
        public Node Left;
        public Node Right;
        public void DisplayNode()
        {
            Console.WriteLine(Data + " ");
        }
    }

下面是插入方法

public class BinarySearchTree
{
        //根
        public Node root;

        public BinarySearchTree()
        {
            root = null;
        }
}

        public void Insert(int i)
        {
            Node newNode = new Node();
            newNode.Data = i;
            //如果根节点没数据
            if (root == null)
            {
                root = newNode;
            }
            else
            {
                Node current = root;
                Node parent;
                while (true)
                {
                    parent = current;
                    if (i < current.Data)
                    {
                        current = current.Left;
                        if (current == null)
                        {
                            parent.Left = newNode;
                            break;
                        }
                    }
                    else
                    {
                        current = current.Right;
                        if (current == null)
                        {
                            parent.Right = newNode;
                            break;
                        }
                    }
                }
            }
        }

 

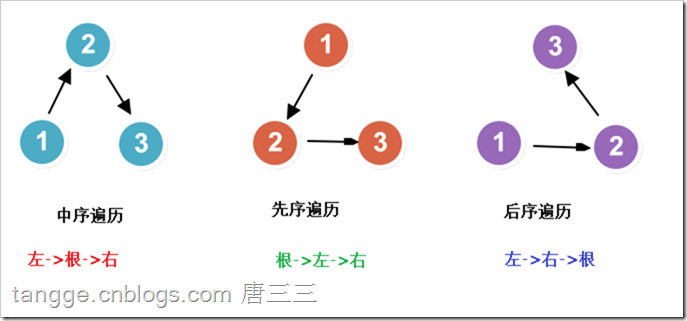
9.2.2.遍历二叉查找树

 

中序遍历

 

既然这个方法是按照升序方式访问每一个节点，所以此方法必须访问到每棵子树的左节点和右节点，

跟着是访问根节点的左子节点下的子树，再接着是访问根节点的右子节点下的子树

//中序遍历
        public void InOrder(Node theRoot)
        {
            if (theRoot != null)
            {
                InOrder(theRoot.Left);
                theRoot.DisplayNode();//显示
                InOrder(theRoot.Right);
            }
        }

 

先序遍历

 

//先序遍历
        public void PreOrder(Node theRoot)
        {
            if (!(theRoot == null))
            {
                theRoot.DisplayNode();
                PreOrder(theRoot.Left);
                PreOrder(theRoot.Right);
            }
        }

 

 

 

后序遍历

 

//后续遍历
        public void PostOrder(Node theRoot)
        {
            if (!(theRoot == null))
            {
                PostOrder(theRoot.Left);
                PostOrder(theRoot.Right);
                theRoot.DisplayNode();
            }
        }

 

9.2.3 在二叉查找树中查找节点和最大/最小值

人们总可以在根节点左子树的最左侧子节点上找到 BST 内的最小值。

public int FindMin()
        {
            Node current = root;
            while (current.Left != null)
                current = current.Left;
            return current.Data;
        }

最大值同理

public int FindMax()
        {
            Node current = root;
            while (current.Right != null)
                current = current.Right;
            return current.Data;
        }

 

查找指定值

public Node Find(int key)
        {
            Node current = root;
            while (current.Data != key)
            {
                if (key < current.Data)
                    current = current.Left;
                else
                current = current.Right;
                if (current == null)
                    return null;
            }
            return current;
        }

 

9.2.4.删除叶子节点

step1”叶子节点：直接删除该节点，再修改其父节点的指针（注意分是根节点和不是根节点）

（例：删除72）

step2”单支节点（即只有左子树或右子树）：让p的子树与p的父亲节点相连，再删除p即可；（注意分是根节点和不是根节点两种情况）

（例：删除79）

step3”节点p的左子树和右子树均不为空：首先找到p的后继y，因为y一定没有左子树，所以可以删除y，并让y的父亲节点成为y的右子树的父亲节点，并用y的值代替p的值；或者可以先找到p的前驱x，x一定没有右子树，所以可以删除x，并让x的父亲节点成为y的左子树的父亲节点。

 

9.2.4.1.删除带有一个子节点的节点

当要删除的节点有一个子节点的时候，需要检查四个条件：

1.这个节点的子节点可能是左子节点；

2.这个节点的子节点可能是右子节点；

3.要删除的这个节点可能是左子节点；

4.要删除的这个节点可能是右子节点。

//如果右子节点为空null
                else if (current.Right == null)
                {
                    //查看是否在根节点上
                    if (current == root)
                        root = current.Left;
                    else if (isLeftChild)
                        parent.Left = current.Left;
                    else
                        parent.Right = current.Right;
                }
                //如果左子节点为空
                else if (current.Left == null)
                {
                    if (current == root)
                        root = current.Right;
                    else if (isLeftChild)
                        parent.Left = parent.Right;
                    else
                        parent.Right = current.Right;
                }

说明：

 

9.2.4.2.删除带有两个子节点的节点

为了找到后继节点，要到原始节点的右子节点上。根据定义这个节点必须比原始节点大。然后，开始沿着左子节点路径走直到用完节点为止。既然子树（像一棵树）内的最小值必须是在左子节点路径的末端，沿着这条路径到达末端就会找到大于原始节点的最小节点。

 

后继节点的代码

public Node GetSuccessor(Node delNode)
        {
            //把删除的节点作为继任者的父节点
            Node successorParent = delNode;
            //把删除的节点作为继任者的节点
            Node successor = delNode;
            //当前节点的右子节点
            Node current = delNode.Right;

            while (current != null)
            {
                successorParent = current;
                successor = current;
                current = current.Left;
            }

            //current.Left = null;

            if (successor != delNode.Right)
            {
                //1.把后继节点的右子节点赋值为后继节点的父节点的左子节点
                successorParent.Left = successor.Right;
                //2.要删除节点的右子节点赋值为后继节点的右子节点
                successor.Right = delNode.Right;

                //后继节点的右子节点的左子节点必须设置为空，不然会死循环
                successor.Right.Left = null;
            }
            return successor;
        }

 

两个节点的代码

         else
            {

                Node successor = GetSuccessor(current);

                if (current == root)
                {
                    root = successor;
                }
                else if (isLeftChild)
                {
                    parent.Left = successor;
                }
                else
                {
                    //3.从父节点的右子节点中移除当前节点，并且把它指向后继节点
                    parent.Right = successor;
                }
                //4.从当前节点中移除当前节点的左子节点，并且把它指向后继节点的左子节点
                successor.Left = current.Left;
            }

 

 

完整的删除代码

public bool Delete(int key)
        {
            Node current = root;
            Node parent = root;//让父节点也等于根
            //判断是否为左子节点
            bool isLeftChild = true;
            //循环删除节点
            while (current.Data != key)
            {

                parent = current;
                //值小于当前节点的值，在左字节点查找
                if (key < current.Data)
                {
                    //取左子节点的数据
                    isLeftChild = true;
                    current = current.Left;
                }
                else
                {
                    isLeftChild = false;
                    current = current.Right;
                }
            }
            //如果查找不到，就退出
            if (current == null)
            {
                return false;
            }
            //查看这个节点的左子节点和右子节点是否为空
            if ((current.Left == null) & (current.Right == null))
            {
                //如果是根节点，就把它设置为空
                if (current == root)
                    root = null;
                //如果为左子节点，就把父节点的左子节点设置为空
                else if (isLeftChild)
                    parent.Left = null;

                else//如果为右子节点，就把父节点的右子节点设置为空
                    parent.Right = null;
            }
            //如果右子节点为空null
            else if (current.Right == null)
            {
                //查看是否在根节点上
                if (current == root)
                    root = current.Left;
                else if (isLeftChild)
                    parent.Left = current.Left;
                else
                    parent.Right = current.Right;
            }
            //如果左子节点为空
            else if (current.Left == null)
            {
                if (current == root)
                    root = current.Right;
                else if (isLeftChild)
                    parent.Left = parent.Right;
                else
                    parent.Right = current.Right;
            }
            //左子节点和右子节点都有的情况
            else
            {

                Node successor = GetSuccessor(current);

                if (current == root)
                {
                    root = successor;
                }
                else if (isLeftChild)
                {
                    parent.Left = successor;
                }
                else
                {
                    //3.从父节点的右子节点中移除当前节点，并且把它指向后继节点
                    parent.Right = successor;
                }
                //4.从当前节点中移除当前节点的左子节点，并且把它指向后继节点的左子节点
                successor.Left = current.Left;
            }
            return true;
        }