并查集——HDOJ-1232-畅通工程

　　并查集

　　并查集（Union-Find Sets）是一种非常精巧而实用的集合，集合中的每个元素仍是一个集合，即它是集合的集合。在并查集中的元素（集合）内部进行查找操作以及并查集中的元素（集合）之间的合并操作的时间复杂度均可视为O(1)，它主要用于处理一些不相交集合的合并问题，在合并之前，需要先判断两个元素是否属于同一集合，这就需要用查找操作来实现，即先查找后合并。

　　并查集的原理也比较简单，逻辑上使用树来表示集合，树的每个节点就表示集合中的一个元素，指针指向其直接父节点，根结点对应的元素就是该集合的“代表”，指针指向自己，沿着每个节点的指针不断向上查找，最终就可以找到该树的根节点，即该集合的代表元素。如下图所示。

　　　　　　　　　　　　　　　　　　　　

　　上图有两个集合，其中第一个集合为 {a,b,c,d}，代表元素是 a；第二个集合为 {e,f,g}，代表元素是 e，它们整体是一个并查集 { {a,b,c,d},  {e,f,g} }。

　　假设使用一个足够长的数组来存储集合元素，并查集在初始化时构造出下图的森林，其中每个元素都是一个单元素集合，即父节点是其自身：

　　　　　　　　　　　　　

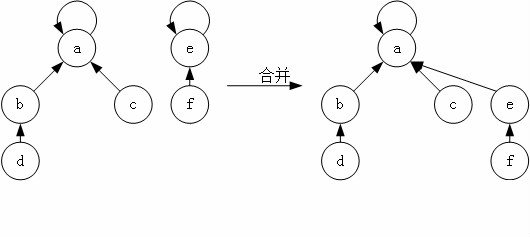
　　并查集内的合并操作非常简单，就是将一个集合的树根指向另一个集合的树根。这里可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界，在合并时，总是将具有较小秩的树根指向具有较大秩的树根。简单的说，就是总是将较矮的树作为子树，添加到较高的树中。如下图所示，第一个集合为 {a,b,c,d}，代表元素是 a，秩为3；第二个集合为 {e,f}，代表元素是 e，秩为2；合并两个集合得到集合 {a,b,c,d,e,f}，代表元素是 a，秩为3。

　　　　　　　　　

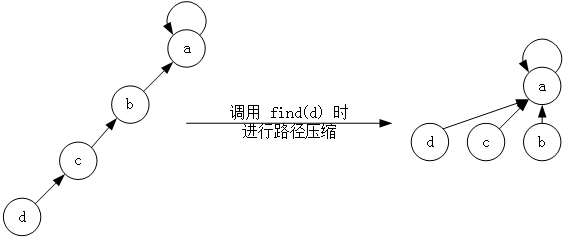
　　对于并查集内的查找操作，其目的就是找到所在集合的代表元素，如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用另一种简单有效的启发式策略——路径压缩。在每次查找时，令查找路径上的每个节点都直接指向我们要找的根节点，如下图所示。

　　　　　　　　　

　　

　　

　　关于并查集，一些常见的用途有求连通子图（判断连通性）、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

　　习题：畅通工程　　

　　题目来源：HDOJ-1232-畅通工程

　　首先在地图上给你若干个城镇，这些城镇都可以看作点，然后告诉你哪些对城镇之间是有道路直接相连的。最后要解决的是整幅图的连通性问题。比如随意给你两个点，让你判断它们是否连通，或者问你整幅图一共有几个连通分支，也就是被分成了几个相互独立的连通子图。像畅通工程这题，问还需要修几条路，实质就是求有几个连通分支。如果有1个连通分支，说明整幅图上的点都连起来了，不需要再修路了；如果有2个连通分支，则只需要再修1条路，从两个连通分支中各选一个点，把它们连起来，那么所有的点都连起来了；如果有3个连通分支，则只需要再修两条路……

　　源码如下：

#include<iostream>
using namespace std;

const int CMAX = ;    // 最多1000个城镇(编号从1开始)

int parent[CMAX];         // 存放各结点的直接父节点，对于根结点，parent指向本身
int Rank[CMAX];           // 存放各结点的秩，即该结点在子树中的高度(实际上只有根结点的秩在按秩合并时才有价值)

int Find(int x)           // 带有路径压缩的查找过程，返回根结点（代表元素）
{
    if (x != parent[x])
        parent[x] = Find(parent[x]);// 沿着查找路径递归向上直到找到根
    return parent[x];               // 找到根，开始回溯，进行路径压缩
}

void Union(int x, int y)    // 按秩合并两个树（集合）,让具有较小秩的根指向具有较大秩的根
{
    int root1 = Find(x);
    int root2 = Find(y);
    if (root1 == root2)     // 根结点相同，无需合并
        return;
    if (Rank[root1] < Rank[root2])
    {
        parent[root1] = root2;
    }
    else
    {
        parent[root2] = root1;
        if (Rank[root1] == Rank[root2]) // 只有秩相等时需要递增根的秩(大树合并小树,根秩不变)
            Rank[root1]++;
    }
}

int main()
{
    int N, M;                              // 城镇数目和道路数目
    while (scanf("%d%d", &N, &M) && N)     // 当N为0时，输入结束
    {
        int tree_num = ;                  // 树的个数，即连通分支数
        for (int i = ; i <= N; i++)       // 初始化每个结点独自成树，秩为1
        {
            parent[i] = i;
            Rank[i] = ;
        }
        int city1, city2;
        for (int i = ; i <= M; i++)       // 读取M条道路,合并连通的城镇
        {
            scanf("%d%d", &city1, &city2);
            Union(city1, city2);
        }
        for (int i = ; i <= N; i++)
        {
            if (parent[i] == i)          // 每找到一个根就有一个连通分支
                tree_num++;
        }
        printf("%d\n", tree_num - );    // 把这些连通分支连起来需要修tree_num-1条路
    }
    return ;
}

　　提交结果：

　　参考资料:　　　《算法导论第3版》—— 21.3 不相交集合森林

　　　　　　　　　　http://blog.csdn.net/dellaserss/article/details/7724401

　　　　　　　　　　http://www.cnblogs.com/cyjb/p/UnionFindSets.html