Codeforces 963A Alternating Sum（等比数列求和+逆元+快速幂）

题目链接：http://codeforces.com/problemset/problem/963/A

题目大意：就是给了你n，a，b和一段长度为k的只有'+'和‘-’字符串，保证n+1被k整除，让你你计算。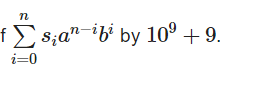

解题思路：

暴力肯定超时的，我们可以先计算出0~k-1这一段的值，当做a1，可以发现如果把每段长度为k的段的值当做一个元素，他们之间是成等比的，比值q=(b/a)^k，

然后就直接用等比数列求和公式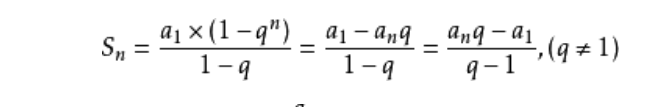求出答案即可。昨天把q当成b/a了，我的脑子啊。。。

注意，判断q==1时不能通过判断a==b，而是判断(a/b)^k==1来实现。

代码：

 #include<cstdio>
 #include<cmath>
 #include<cctype>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<vector>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<string>
 #define lc(a) (a<<1)
 #define rc(a) (a<<1|1)
 #define MID(a,b) ((a+b)>>1)
 #define fin(name)  freopen(name,"r",stdin)
 #define fout(name) freopen(name,"w",stdout)
 #define clr(arr,val) memset(arr,val,sizeof(arr))
 #define _for(i,start,end) for(int i=start;i<=end;i++)
 #define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
 using namespace std;
 typedef long long LL;
 const LL MOD=1e9+;
 const double eps=1e-;
 
 string str;
 
 LL fpow(LL x,LL n){
     LL res=;
     while(n>){
         if(n&) res=res*x%MOD;  //如果二进制最低位为1，则乘上x^(2^i)
         x=x*x%MOD;                //将x平方并取模
         n>>=;
     }
     return (res%MOD+MOD)%MOD;
 }
 
 LL extend_gcd(LL a,LL b,LL &x,LL &y){
     if(!b){
         x=;
         y=;
         return a;
     }
     LL gcd=extend_gcd(b,a%b,x,y);
     LL t=x;
     x=y;
     y=t-(a/b)*x;
     return gcd;
 }
 
 LL NY(LL num){
     LL x,y;
     extend_gcd(num,MOD,x,y);
     return (x%MOD+MOD)%MOD;
 }
 
 int main(){
     FAST_IO;
     LL n,a,b,k;
     cin>>n>>a>>b>>k;
     cin>>str;
     LL len=(n+)/k;
     LL sum=;
     for(int i=;i<k;i++){
         if(str[i]=='+')
             sum=((sum+fpow(a,n-i)*fpow(b,i))%MOD+MOD)%MOD;
         else
             sum=((sum-fpow(a,n-i)*fpow(b,i))%MOD+MOD)%MOD;
     }
     LL ans;
     //注意，比值q是(b/a)^k而不是(b/a)
     LL q=fpow(NY(a),k)*fpow(b,k)%MOD;
     if(q!=){
         LL _q=NY(q-);
         ans=(sum*(fpow(q,len)-)%MOD*_q%MOD+MOD)%MOD;
     }
     else
         ans=sum*len%MOD;
     cout<<ans<<endl;
     return ;
 }